Compressible Helical Beltrami Flow

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
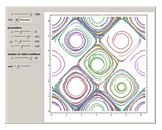
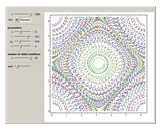
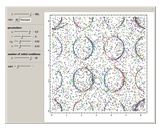
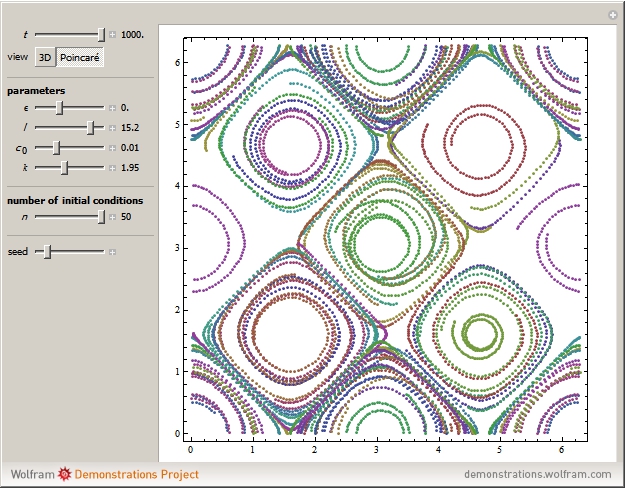
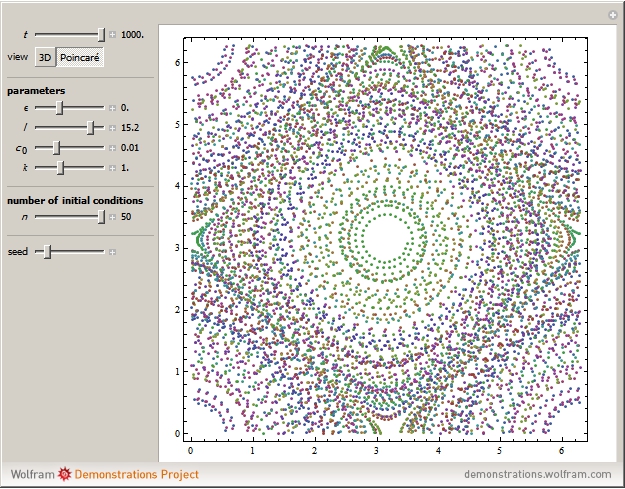
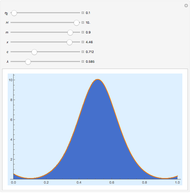
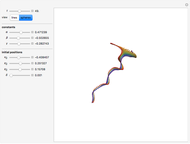
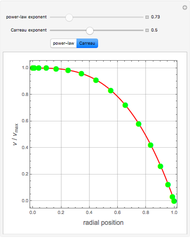
Consider the case of a compressible fluid undergoing helical (Beltrami) flow with nonuniform vorticity and velocity. This is a generalization of the ABC (Arnold–Beltrami–Childress) flow for the compressible case [1] in which chaotic dynamics appear [2] that involve a "Q-flow" (flows with quasisymmetry).
Contributed by: Enrique Zeleny (June 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Q-flows have a Hamiltonian  ; then
; then
 ,
,
 ,
,
 ,
,
where  is a perturbation parameter (when
is a perturbation parameter (when  the advection equations are integrable) and
the advection equations are integrable) and

with  and
and  .
.
Now, introducing a soliton-like function  related to the Beltrami flow condition
related to the Beltrami flow condition  for a scalar function
for a scalar function  (condition for compressibility), in this case of the form
(condition for compressibility), in this case of the form

where the variable  is used instead of
is used instead of  and are related according to
and are related according to  ,
,  is a constant, and
is a constant, and  is a scale parameter along
is a scale parameter along  . Consider a generating function of the type
. Consider a generating function of the type
 ;
;
then, rewriting the equations, we have
 ,
,
 ,
,
 .
.
References
[1] A. Morgulis, V. I. Yudovich, and G. M. Zaslavsky, "Compressible Helical Flows," Communications on Pure and Applied Mathematics, 48(5), 2006 pp. 571–582. doi:10.1002/cpa.3160480505
[2] G. M. Zaslavsky, Hamiltonian Chaos and Fractional Dynamics, New York: Oxford University Press, 2005.
Permanent Citation