Cubic Spline Interpolation versus Interpolating Polynomial

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
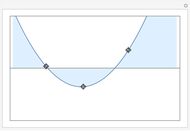
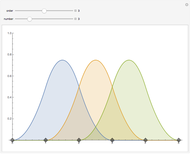
Given  equally spaced sample values of a function
equally spaced sample values of a function  , one can approximate
, one can approximate  as the polynomial of degree
as the polynomial of degree  that passes through all
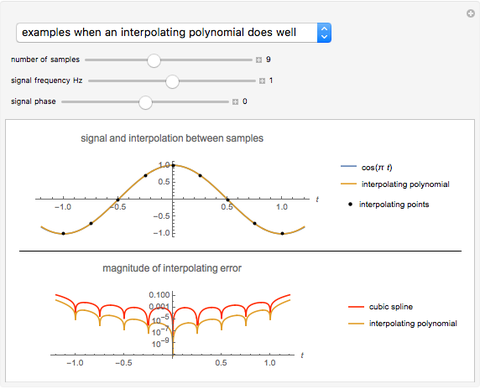
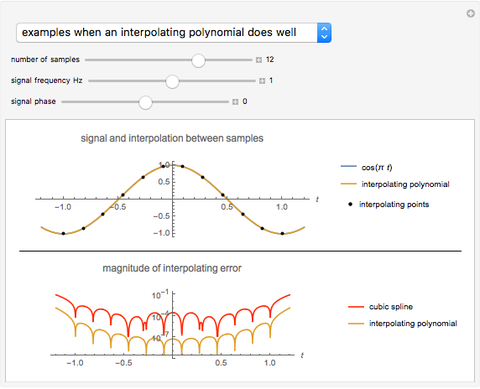
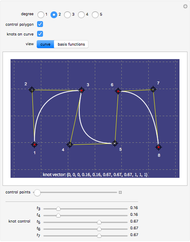
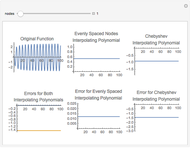
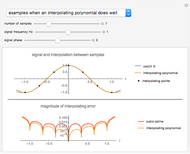
that passes through all  points on a plot. Runge's phenomenon tells us that such an approximation often has large oscillations near the ends of the interpolating interval. On the other hand, cubic spline interpolation is often considered a better approximation method because it is not prone to such oscillations. However, if the sample rate is sufficiently high relative to highest frequency in the signal, then an interpolating polynomial has a smaller approximation error than a cubic spline interpolation.
points on a plot. Runge's phenomenon tells us that such an approximation often has large oscillations near the ends of the interpolating interval. On the other hand, cubic spline interpolation is often considered a better approximation method because it is not prone to such oscillations. However, if the sample rate is sufficiently high relative to highest frequency in the signal, then an interpolating polynomial has a smaller approximation error than a cubic spline interpolation.
Contributed by: Ted Ersek (April 2017)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference
[1] Wikiversity. "Cubic Spline Interpolation." (Apr 5, 2017) en.wikiversity.org/wiki/Cubic_Spline_Interpolation.
Permanent Citation
"Cubic Spline Interpolation versus Interpolating Polynomial"
http://demonstrations.wolfram.com/CubicSplineInterpolationVersusInterpolatingPolynomial/
Wolfram Demonstrations Project
Published: April 10 2017