Cylinder Area Paradox
Initializing live version

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
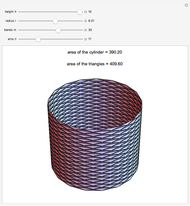
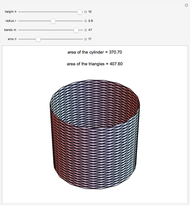
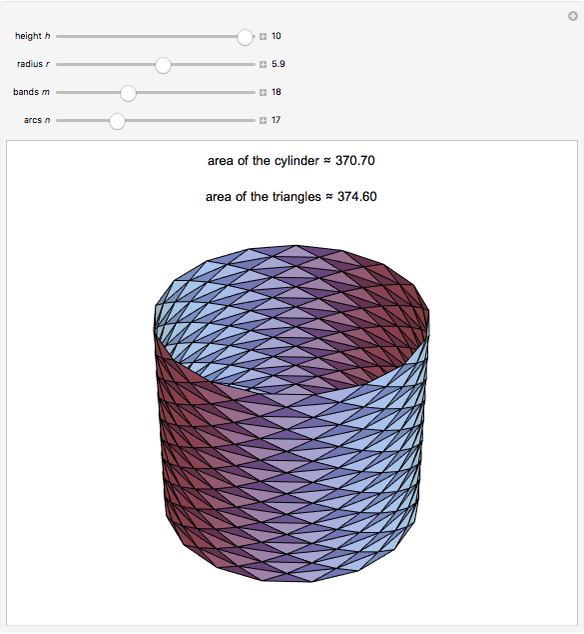
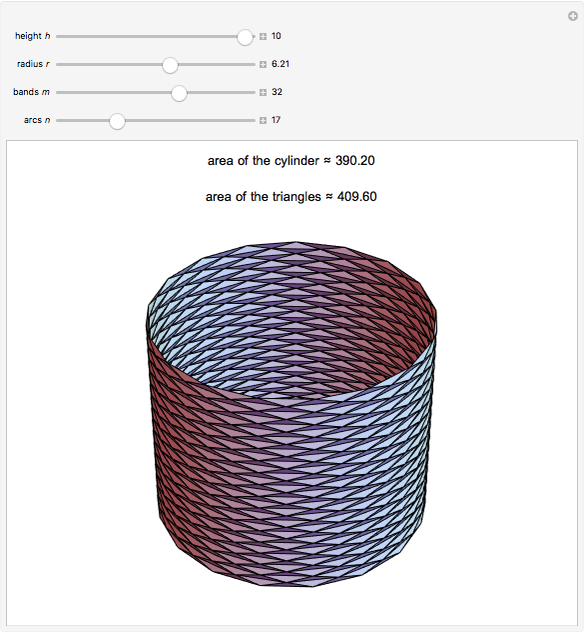
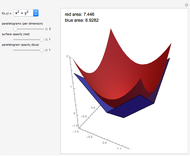
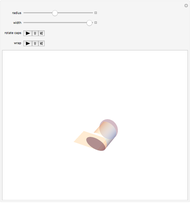
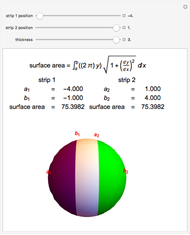
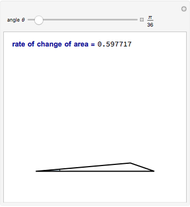
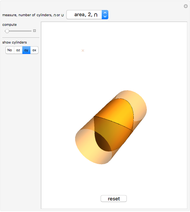
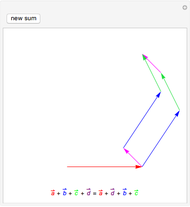
Let  be the surface of a cylinder of height
be the surface of a cylinder of height  and radius
and radius  . (
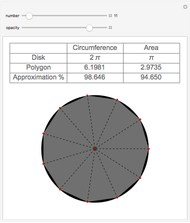
. ( does not include the flat circular ends of the cylinder.) This Demonstration constructs a set of triangles that tend uniformly to
does not include the flat circular ends of the cylinder.) This Demonstration constructs a set of triangles that tend uniformly to  —yet their total area does not tend to the area of
—yet their total area does not tend to the area of  !
!
Contributed by: George Beck and Izidor Hafner (November 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For details, see Freida Zames' Surface Area and the Cylinder Area Paradox.
Permanent Citation