Discrepancy Conjecture

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
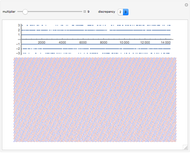
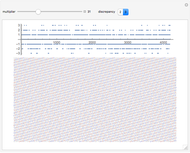
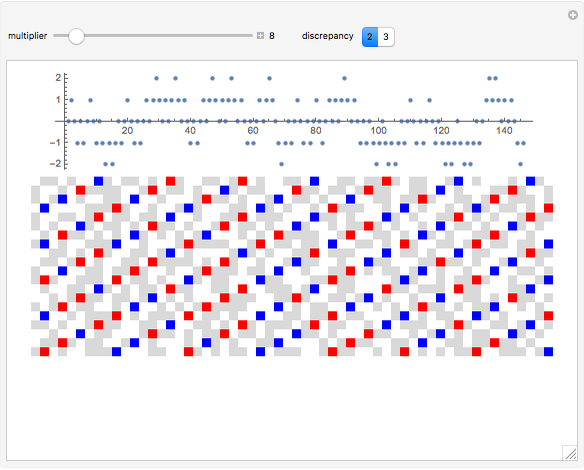
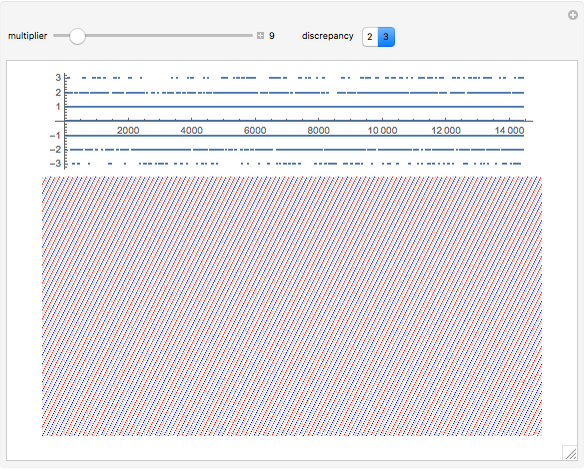
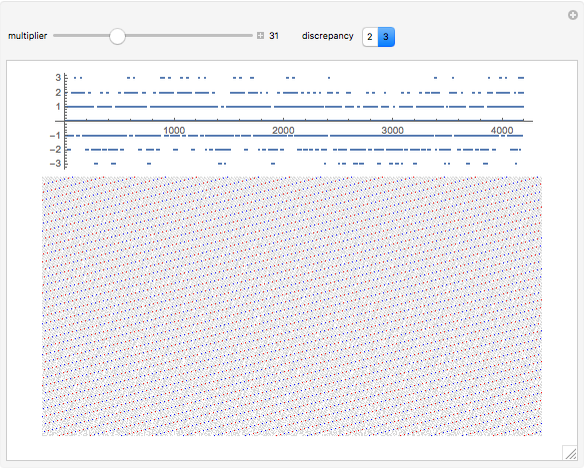
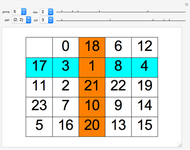
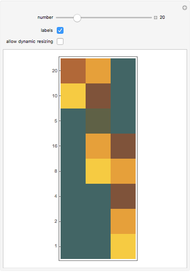
In 2015, Terence Tao proved the Erdős discrepancy conjecture [1]. Consider a sequence like  , where all the terms are
, where all the terms are  . After that, partition
. After that, partition  into sections of length
into sections of length  , take the first
, take the first  sections, and then total up the last terms in each section. For
sections, and then total up the last terms in each section. For  and
and  , the sections are
, the sections are  ,
,  ,
,  , and
, and  ; the final terms are
; the final terms are  ; and their total is 2. The maximum value obtained by any considered
; and their total is 2. The maximum value obtained by any considered  or
or  is the discrepancy.
is the discrepancy.
Contributed by: Ed Pegg Jr (October 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] T. Tao, "The Erdős Discrepancy Problem," 2015. arXiv:1509.05363.
[2] B. Konev and A. Lisitsa, "A SAT Attack on the Erdős Discrepancy Conjecture," in Theory and Applications of Satisfiability Testing—SAT 2014, 8561, 2014 pp. 219–226.
[3] B. Konev and A. Lisitsa, "Computer-Aided Proof of Erdős Discrepancy Properties," Artificial Intelligence, 224, 2015 pp. 103–118. Data.
[4] "The Erdős Discrepancy Problem." Polymath. (Sep 21, 2015) michaelnielsen.org/polymath1/index.php?title=The_Erdős _discrepancy _problem.
[5] Wikipedia. "±1 Sequence." (Sep 30, 2015) en.wikipedia.org/wiki/%C2 % B11-sequence.
Permanent Citation