Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

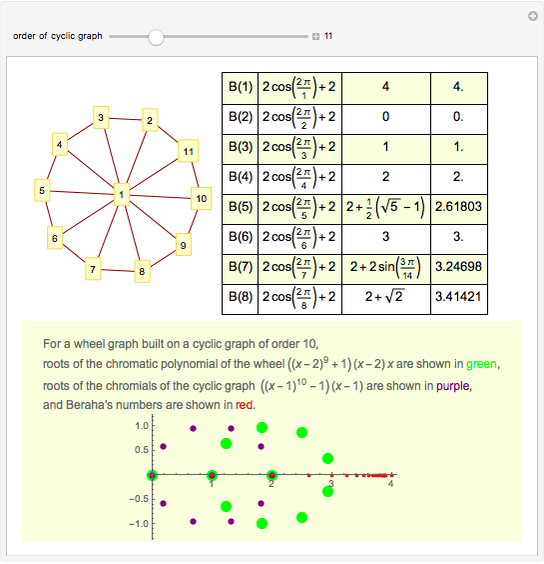
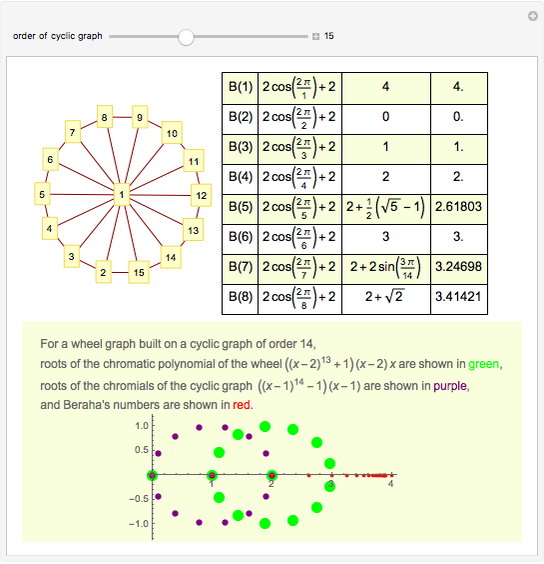
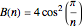Beraha's Conjecture, Wheels, and Cyclic Graphs

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

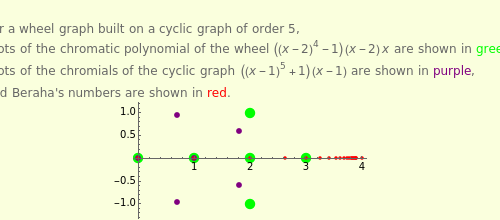
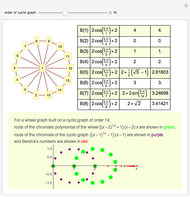
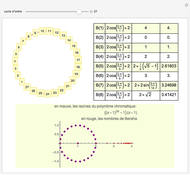
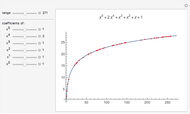
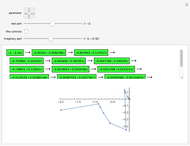
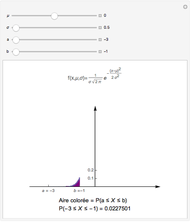
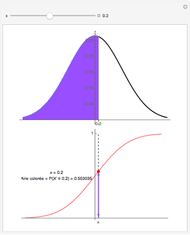
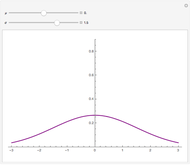
A graph coloring assigns colors to the vertices of a graph in such a way that a pair of vertices joined by an edge do not get the same color. The chromatic polynomial of a graph gives the number of ways of coloring the graph with colors.

[more]

Beraha's numbers are . Tutte conjectured that there is a link between Beraha's numbers and some classes of graphs.

This Demonstration shows that for a small number of vertices, it is not obvious what the connection is between the roots of the chromatic polynomial of a cyclic graph (green), the roots of the chromatic polynomial of the corresponding wheel graph (purple), and Beraha's numbers (red).

However, taking more vertices clearly shows a relationship between these three sets of numbers.

[less]

Contributed by: Jacqueline Zizi (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send