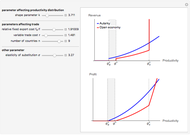
Dynamics in the Solow-Swan Growth Model

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
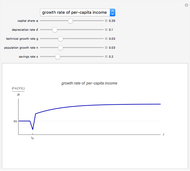
The Solow–Swan model is a simple neoclassical growth model. It postulates that growth of per-capita output is the result of capital accumulation and/or technological progress. As soon as the economy reaches its steady state, per-capita output growth is only possible via technological progress, which is exogenous in the model.
[more]
Contributed by: Richard Foltyn (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
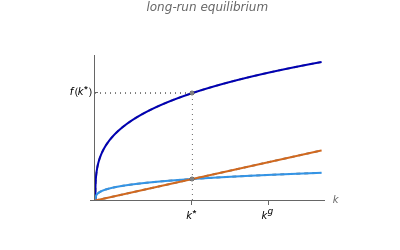
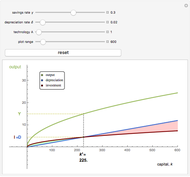
Formally, the main aspects of the Solow–Swan model can be derived from the differential equation that describes capital accumulation:  . Capital (per effective labor) accumulates if the proportion of output saved (and thus invested) is higher than the break-even investment, defined as the amount of capital needed to cover depreciation
. Capital (per effective labor) accumulates if the proportion of output saved (and thus invested) is higher than the break-even investment, defined as the amount of capital needed to cover depreciation  , population growth
, population growth  , and technological progress
, and technological progress  . In the steady state, capital per effective labor
. In the steady state, capital per effective labor  is constant by definition and hence
is constant by definition and hence  . The standard Cobb–Douglas production function is used in this Demonstration, so its intensive form is defined as
. The standard Cobb–Douglas production function is used in this Demonstration, so its intensive form is defined as  , where
, where  is the elasticity of capital.
is the elasticity of capital.
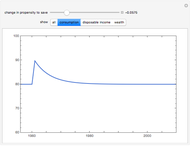
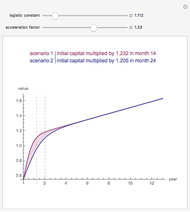
It is evident from the model dynamics that only a change in the rate of technological progress  has any influence on the long-run growth rate of per-capita output and consumption. For any other parameter change, the growth rate eventually converges back to the original value of
has any influence on the long-run growth rate of per-capita output and consumption. For any other parameter change, the growth rate eventually converges back to the original value of  .
.
References:
[1] R. J. Barro and X. Sala-i-Martin, "Growth Models with Exogenous Saving Rates (The Solow–Swan Model)," Economic Growth, 2nd ed., Cambridge, MA: MIT University Press, 2004 pp. 14-58.
[2] D. Romer, "The Solow Growth Model," Advanced Macroeconomics, 3rd ed., New York: McGraw–Hill, 2006.
[3] R. M. Solow, "Contribution to the Theory of Economic Growth," The Quarterly Journal of Economics, 70(1), 1956 pp. 65–94.
[4] T. W. Swan, "Economic Growth and Capital Accumulation," Economic Record, 32, 1956.
Permanent Citation