Eigenvalue Plots of Certain Tridiagonal Matrices

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
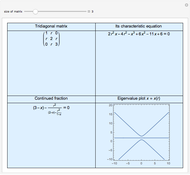
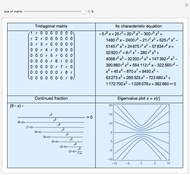
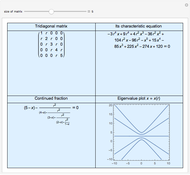
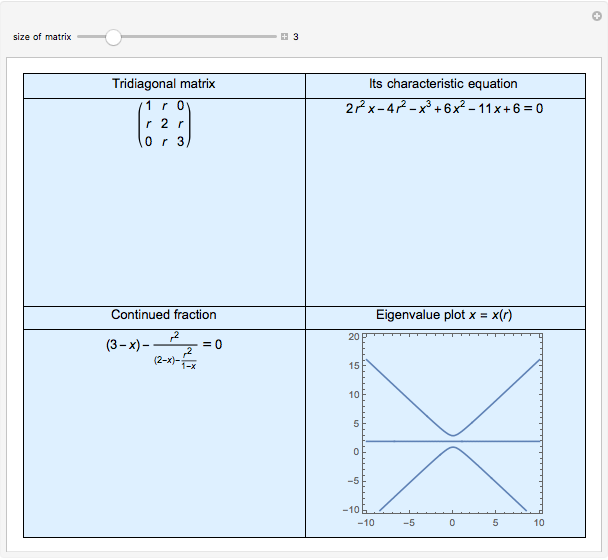
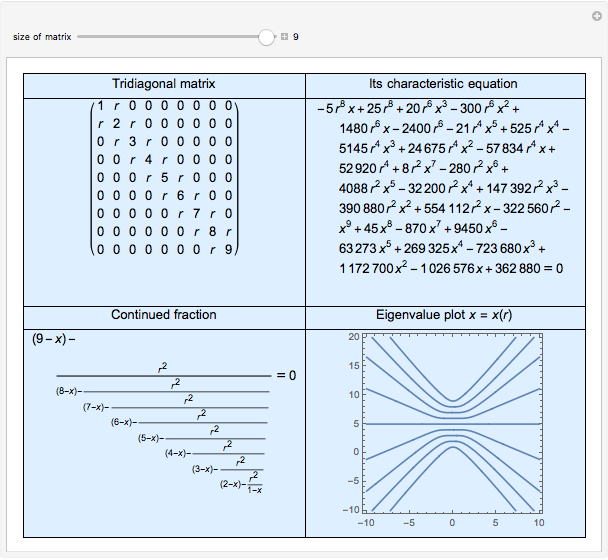
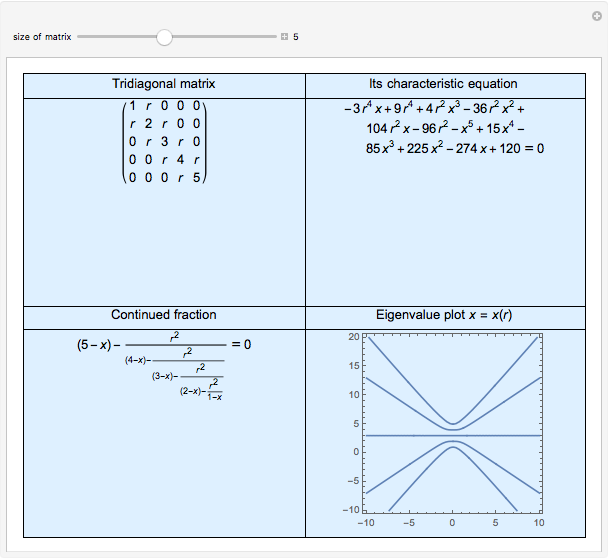
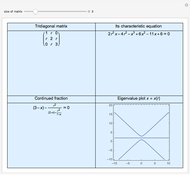
It is easy to calculate the determinant of a tridiagonal matrix inductively. However, finding the eigenvalues is more challenging. This Demonstration illustrates the eigenvalue plots of the tridiagonal matrix whose entries depend on a real parameter  . Explore the interesting pattern that emerges when the eigenvalues are plotted against that parameter. Note the difference between plots when the size of the matrix is odd or even. Is there a lower or upper bound for these curves?
. Explore the interesting pattern that emerges when the eigenvalues are plotted against that parameter. Note the difference between plots when the size of the matrix is odd or even. Is there a lower or upper bound for these curves?
Contributed by: Nail Ussembayev (Indiana University) (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Consider a square matrix  with entries
with entries  , where
, where  is a variable real parameter and
is a variable real parameter and  is the Kronecker delta. Since
is the Kronecker delta. Since  for all
for all 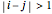 , we call such a matrix a tridiagonal matrix. If we define
, we call such a matrix a tridiagonal matrix. If we define  ,
,  for
for  , then obviously
, then obviously  is the characteristic polynomial of
is the characteristic polynomial of  . One can verify that these polynomials satisfy a recurrence relation
. One can verify that these polynomials satisfy a recurrence relation 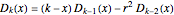 and that they are associated with continued fractions, namely
and that they are associated with continued fractions, namely 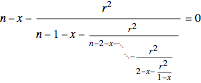 .
.
Permanent Citation