Functions of Matrices

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
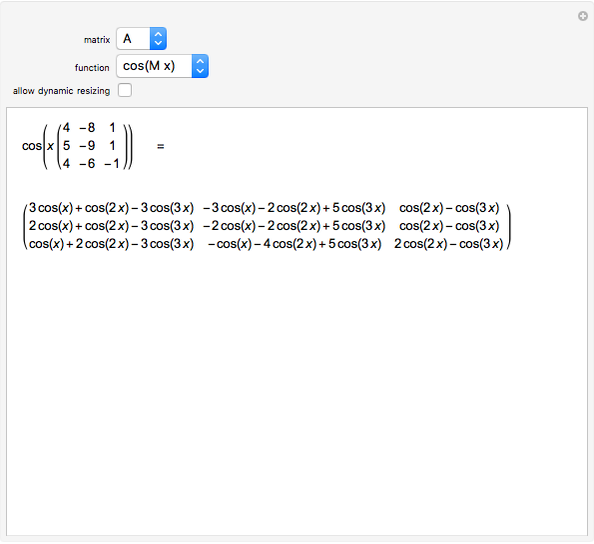
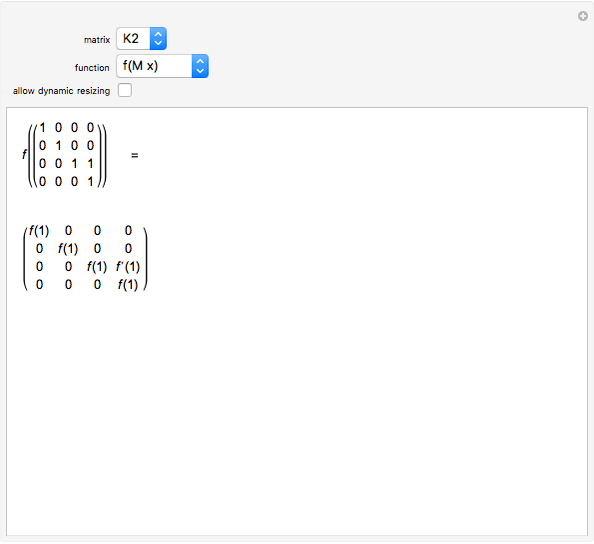
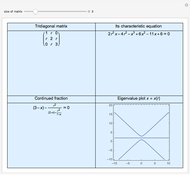
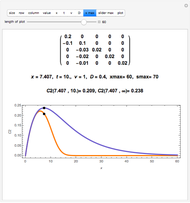
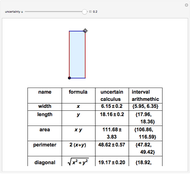
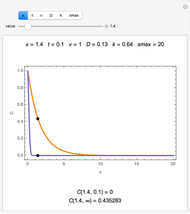
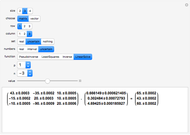
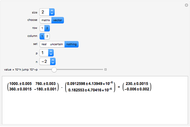
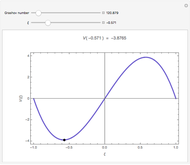
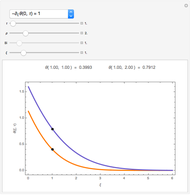
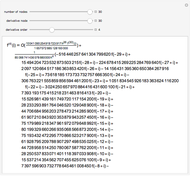
This Demonstration computes some standard functions of a set of rather arbitrary matrices. The test matrix 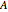 has distinct eigenvalues; the matrices
has distinct eigenvalues; the matrices 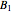 and
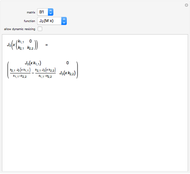
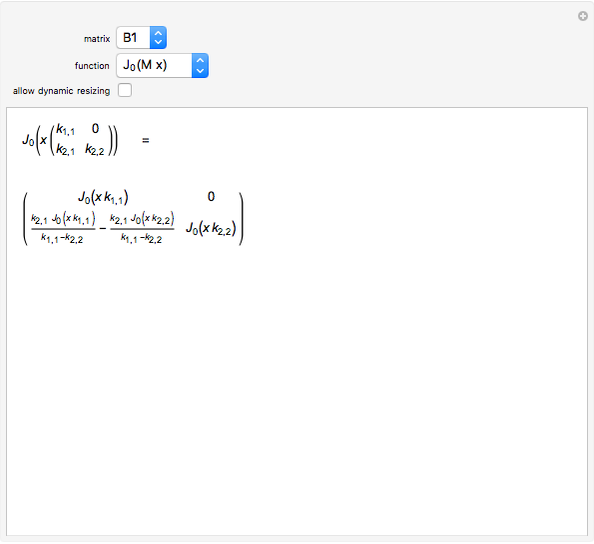
and 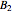 are symbolic, but triangular with different and multiple eigenvalues; the matrices
are symbolic, but triangular with different and multiple eigenvalues; the matrices  to
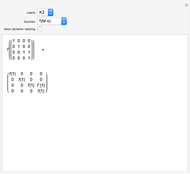
to  are numeric with the same multiple eigenvalues but different Jordan decomposition forms;
are numeric with the same multiple eigenvalues but different Jordan decomposition forms; 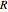 is a numerical random matrix.
is a numerical random matrix.
Contributed by: Mikhail Dimitrov Mikhailov (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Different methods of computing a function of a matrix are described in: F. R. Gantmacher, The Theory of Matrices, trans. K. A. Hirsch, 2 vols., New York: Chelsea Publishing Company, 1959.
This Demonstration uses the matrix exponential of a matrix with no zero eigenvalues to compute an arbitrary function 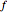 of the matrix. Replacing
of the matrix. Replacing 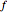 by sin, cos,
by sin, cos, 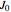 ,
,  ,
, 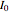 ,
, 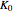 , or erf computes the corresponding function of the matrix.
, or erf computes the corresponding function of the matrix.
The matrix 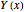 satisfies the matrix differential equation:
satisfies the matrix differential equation:
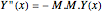 if
if  or
or 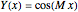 ,
,
 if
if  or
or  ,
,
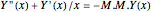 if
if 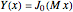 or
or 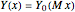 ,
,
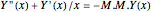 if
if 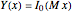 or
or 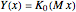 ,
,
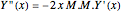 if
if 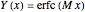 .
.
Permanent Citation