Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

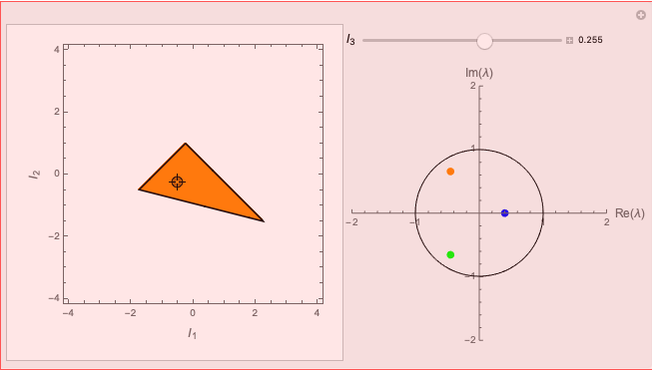
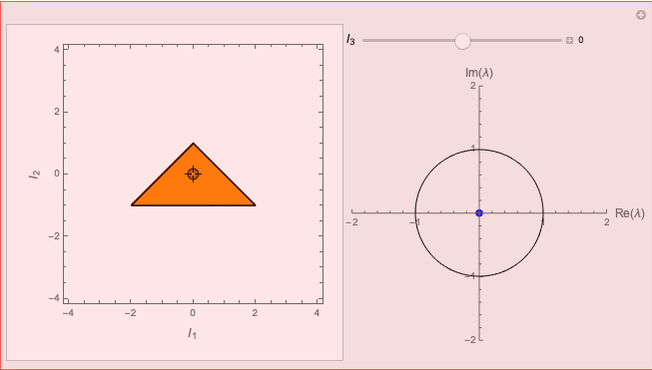
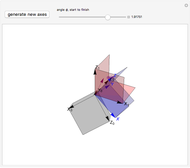
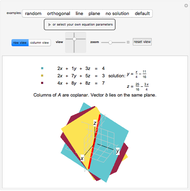
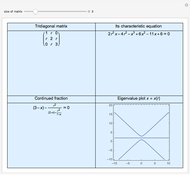
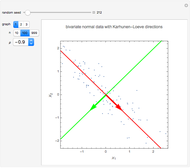
Eigenvalues and the Principal Invariants of a Linear Map

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

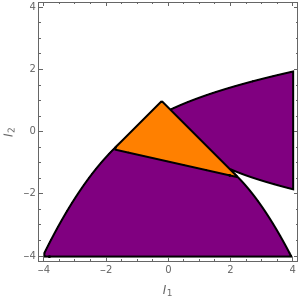
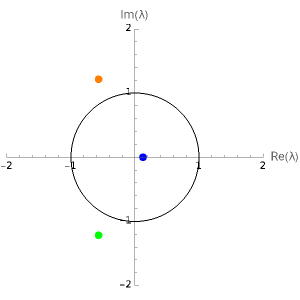
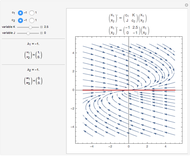
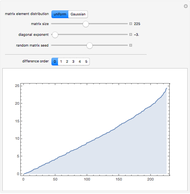
The quantities , , are called the principal invariants of the matrix .

[more]

Drag the point in the - plane and move the slider to display the corresponding eigenvalues around the unit circle in the complex plane.

In the left-hand graphic, the discriminant is negative in the purple region; in the orange region, the eigenvalues have modulus less than one.

The eigenvalues of the matrix determine how the flow of a differential map or the orbit of a discrete map behaves.

[less]

Contributed by: George Shillcock (March 2019)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send