Einstein Solid

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
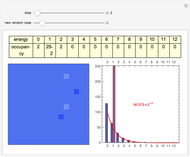
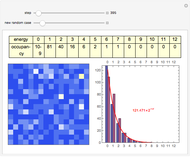
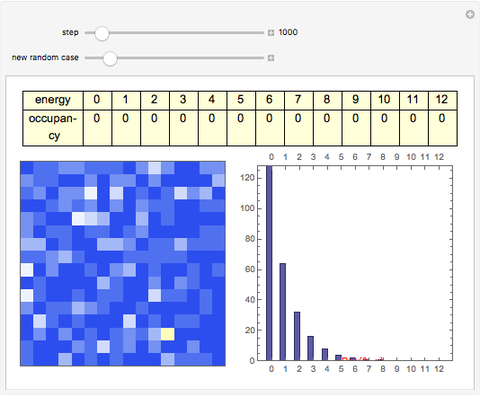
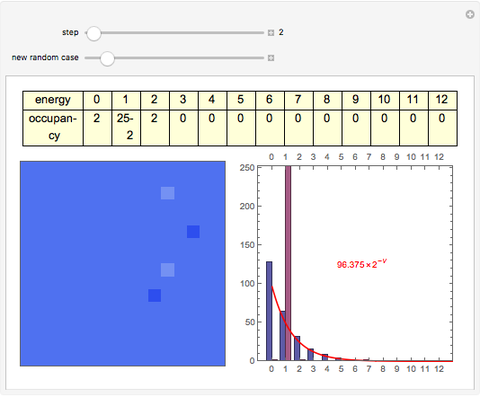
The 2D array on the left is a simplified model of a solid, where each cell represents an oscillator whose energy is some multiple of ℏω. In the initial state, the energy of each cell is exactly ℏω. At each successive step, one quantum of energy is transferred between two randomly chosen cells. After about 20,000 steps, the distribution of energies closely approximates the Boltzmann distribution and thermal equilibrium is obtained.
Contributed by: Enrique Zeleny (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
At low temperatures, the Dulong–Petit law fails and the specific heat  of solid is no longer constant. The Einstein quantum model for a solid correctly explains this phenomenon. We can make a simplified model of a solid with a 2D cell array (Black and Ogborn, 1976) with one oscillator in each cell with an energy of a multiple of ℏω, and thermal interaction reproduced through a transfer of a quantum of energy between a pair of these cells chosen randomly. The number of points assigned to each cell is the number of quanta possessed by the oscillator (occupancy). The initial state assigns one quantum to every cell. After about 1,000 steps, the distribution of a thermal equilibrium state and Boltzmann distribution is obtained; it is stable after more steps. Blue bars represent instantaneous values
of solid is no longer constant. The Einstein quantum model for a solid correctly explains this phenomenon. We can make a simplified model of a solid with a 2D cell array (Black and Ogborn, 1976) with one oscillator in each cell with an energy of a multiple of ℏω, and thermal interaction reproduced through a transfer of a quantum of energy between a pair of these cells chosen randomly. The number of points assigned to each cell is the number of quanta possessed by the oscillator (occupancy). The initial state assigns one quantum to every cell. After about 1,000 steps, the distribution of a thermal equilibrium state and Boltzmann distribution is obtained; it is stable after more steps. Blue bars represent instantaneous values  , purple bars represent the mean values given by the canonical distribution
, purple bars represent the mean values given by the canonical distribution  (equal to
(equal to  ), and the red curve represents the fit of the occupancies.
), and the red curve represents the fit of the occupancies.
Permanent Citation
"Einstein Solid"
http://demonstrations.wolfram.com/EinsteinSolid/
Wolfram Demonstrations Project
Published: March 7 2011