Enumerating Cycles of a Directed Graph

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
Contributed by: Daniel Skates (November 2010)
Open content licensed under CC BY-NC-SA
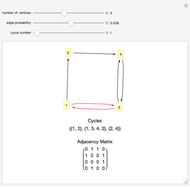
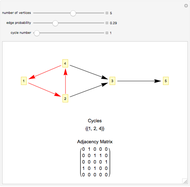
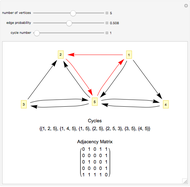
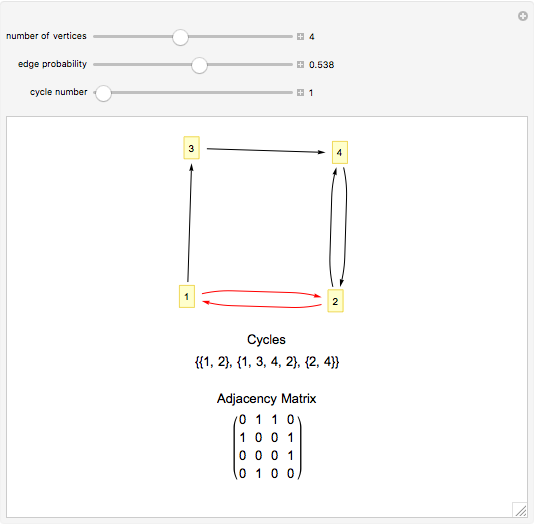
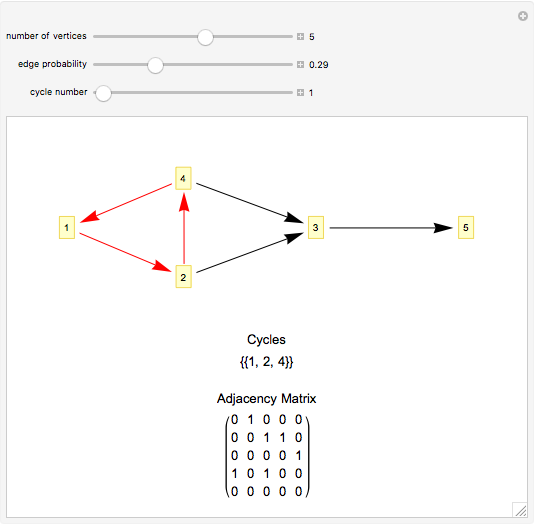
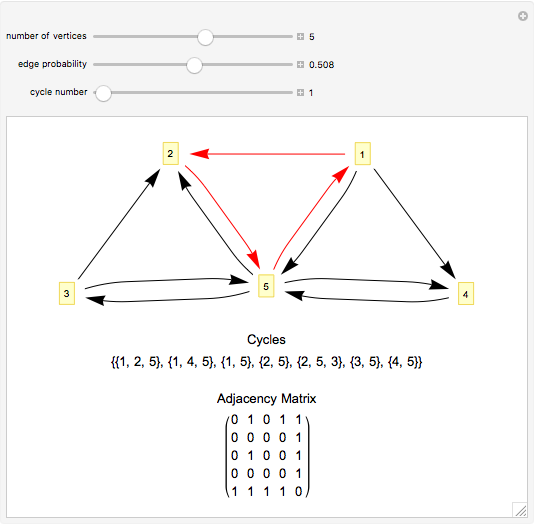
Snapshots
Details
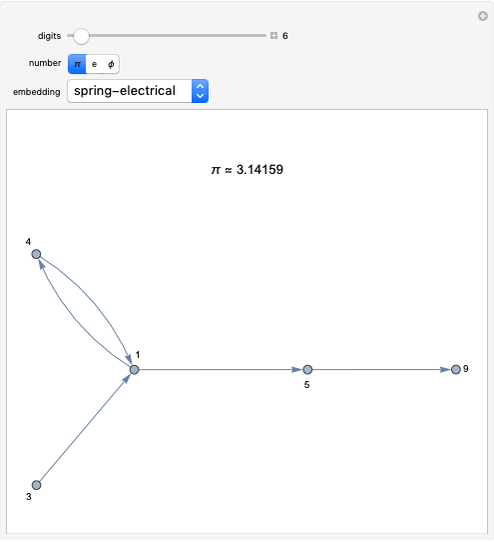
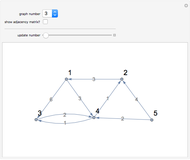
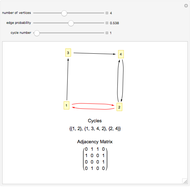
This Demonstration implements Johnson's algorithm, finding all the distinct elementary cycles in a graph, and generates random directed graphs.
An elementary cycle in a directed graph is a sequence of vertices  in the graph such that for
in the graph such that for  , there exists an edge from
, there exists an edge from  to
to  , as well as one from
, as well as one from  to
to  , and that no vertex appears more than once in the sequence. Two elementary cycles are distinct if one is not a cyclic permutation of the other.
, and that no vertex appears more than once in the sequence. Two elementary cycles are distinct if one is not a cyclic permutation of the other.
Note that Mathematica 7 does not have a native circuit finding method.
Reference
[1] D. B. Johnson, "Finding All the Elementary Circuits of a Directed Graph," SIAM Journal of Computing, 4(1), 1975 pp. 77–84. http://epubs.siam.org/doi/pdf/10.1137/0204007.
Permanent Citation