Folding Nets for Some Golden Rhombic Solids

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
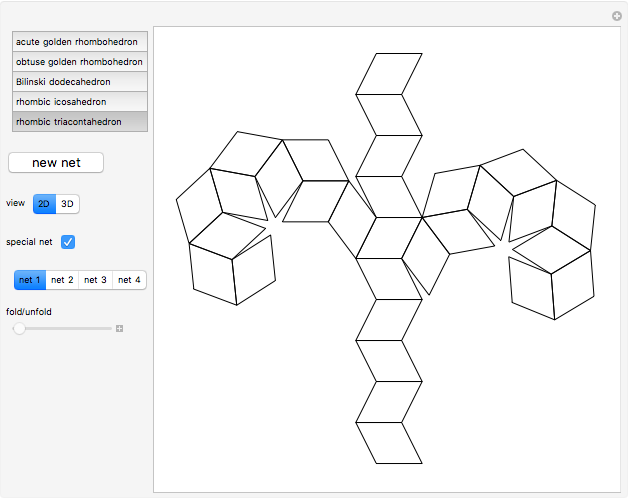
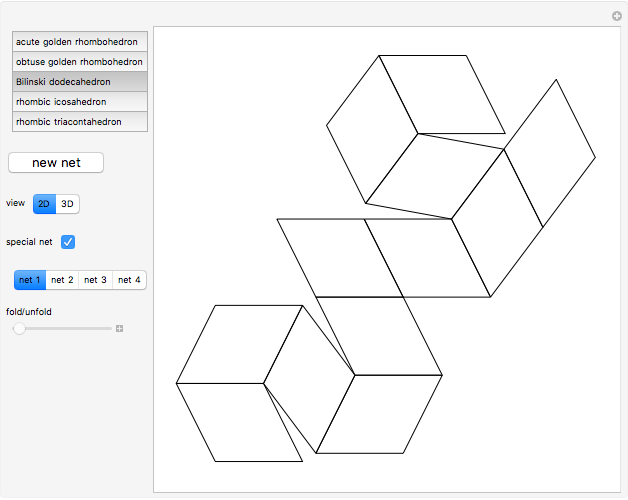
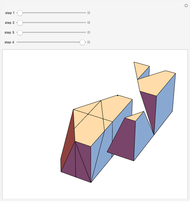
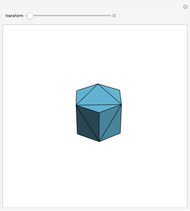
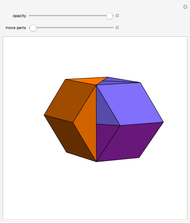
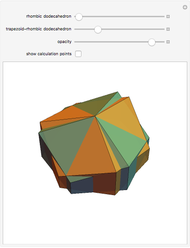
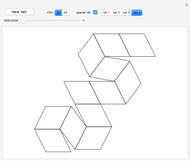
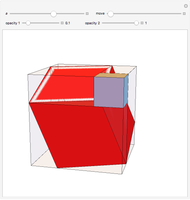
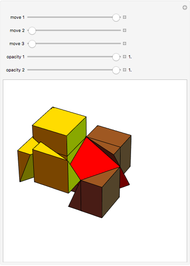
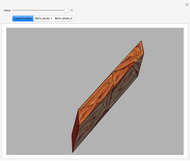
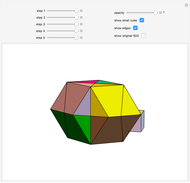
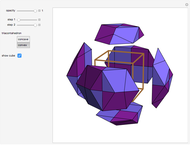
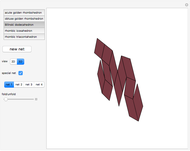
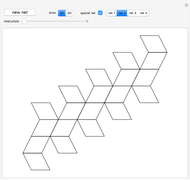
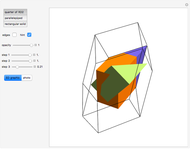
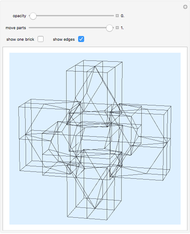
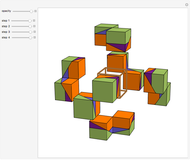
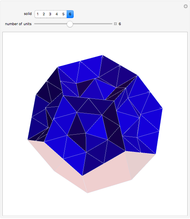
This Demonstration shows nets for some golden rhombic solids. The viewpoint changes as the net closes.
Contributed by: Izidor Hafner (February 2019)
Open content licensed under CC BY-NC-SA
Details
The diagonals of length  and
and  in a golden rhombus are in the ratio
in a golden rhombus are in the ratio  , where
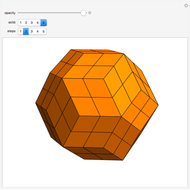
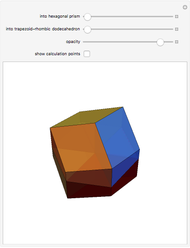
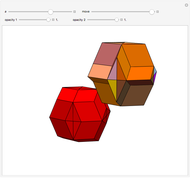
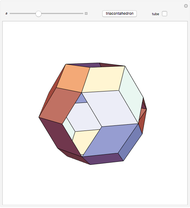
, where  is the golden ratio. The faces of the acute golden rhombohedron, Bilinski dodecahedron, obtuse golden rhombohedron, rhombic icosahedron and rhombic triacontahedron are all golden rhombi [1]. These are the only convex solids that have golden rhombic faces [2, pp. 151–156].
is the golden ratio. The faces of the acute golden rhombohedron, Bilinski dodecahedron, obtuse golden rhombohedron, rhombic icosahedron and rhombic triacontahedron are all golden rhombi [1]. These are the only convex solids that have golden rhombic faces [2, pp. 151–156].
Find more on nets in [3]. For more about nonconvex golden rhombic solids see [4, 5] .
References
[1] E. W. Weisstein. "Golden Rhombus" from Wolfram MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/GoldenRhombus.html (Wolfram MathWorld).
[2] P. R. Cromwell, Polyhedra, New York: Cambridge University Press, 1997.
[3] M. Friedman, A History of Folding in Mathematics: Mathematizing the Margins, New York, NY: Springer International Publishing, 2018.
[4] I. Hafner and T. Zitko. "Introduction to Golden Rhombic Polyhedra." (Feb 18, 2019) www.mi.sanu.ac.rs/vismath/hafner2/IntrodRhombic.html.
[5] I. Hafner and D. Felda. "Rhombic Polyhedra" (in Slovenian). (Feb 18, 2019) www.logika.si/poliedriCDsl/Zlati_rombski_poliedri.pdf.
Snapshots
Permanent Citation