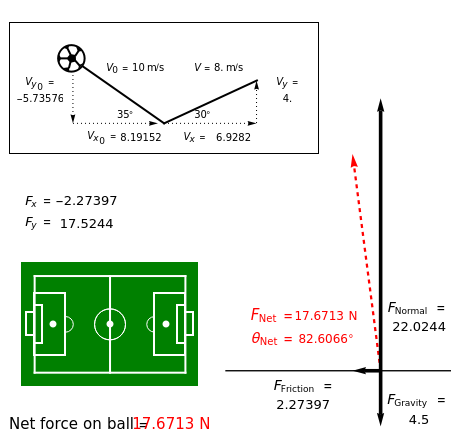
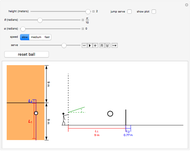
Forces on a Bouncing Ball

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
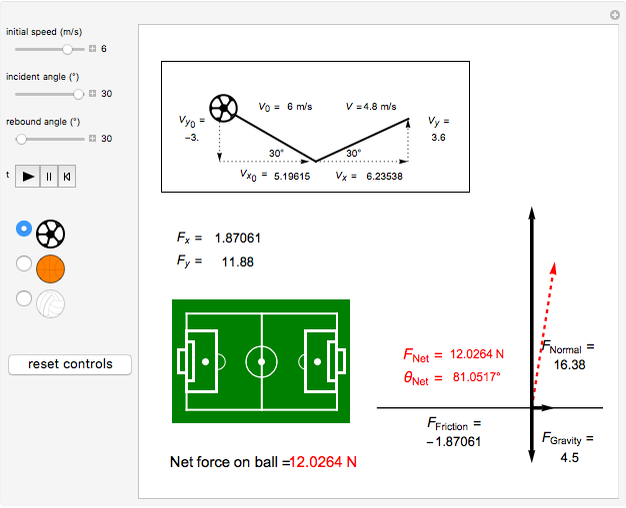
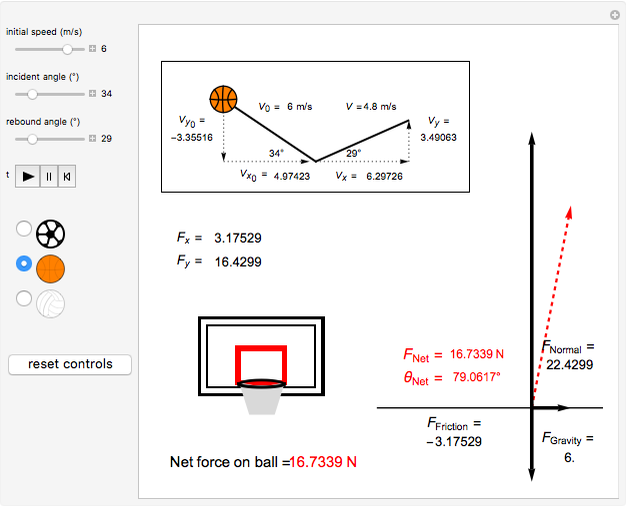
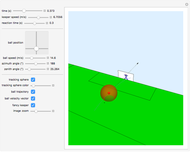
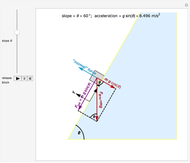
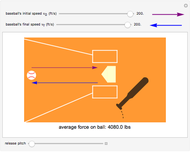
A ball flies through the air, hits the ground, and bounces back up. You can choose a soccer ball, basketball, or volleyball, and select the initial velocity, angle of incidence, and angle of rebound to determine the forces on the ball when it hits the ground. The coefficient of restitution  for each type of ball is estimated as 0.8, which means that the vertical velocity is reduced by 20% after impact with the ground. Frictional forces also reduce the horizontal velocity of the ball. The frictional and normal forces are found from the input values, using the change of momentum component with time
for each type of ball is estimated as 0.8, which means that the vertical velocity is reduced by 20% after impact with the ground. Frictional forces also reduce the horizontal velocity of the ball. The frictional and normal forces are found from the input values, using the change of momentum component with time  ,
, 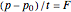 .
.
Contributed by: Anissa Dadkhah (June 2015)
Based on a problem by William Harvie (Torrey Pines AP Physics C)
Open content licensed under CC BY-NC-SA
Snapshots
Details
 is the coefficient of restitution =
is the coefficient of restitution =  , where
, where 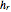 is the rebound height and
is the rebound height and 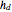 is the drop height.
is the drop height.
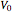 is the initial total velocity.
is the initial total velocity.
 is the initial vertical velocity.
is the initial vertical velocity.
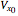 is the initial horizontal velocity.
is the initial horizontal velocity.
 is the final total velocity.
is the final total velocity.
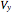 is the final vertical velocity.
is the final vertical velocity.
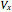 is the final horizontal velocity.
is the final horizontal velocity.
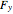 is the net vertical force.
is the net vertical force.
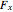 is the net horizontal force.
is the net horizontal force.
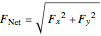 .
.
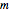 is the mass.
is the mass.
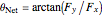 .
.
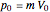 is the initial momentum.
is the initial momentum.
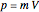 is the final momentum.
is the final momentum.
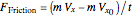 .
.
 .
.
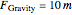 .
.
Permanent Citation