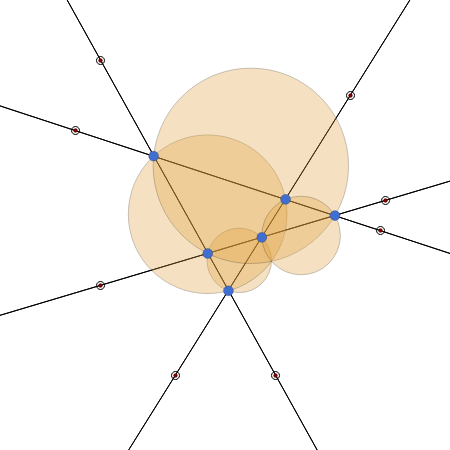
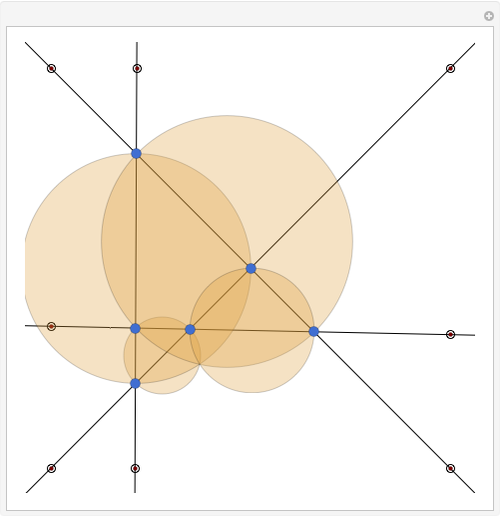
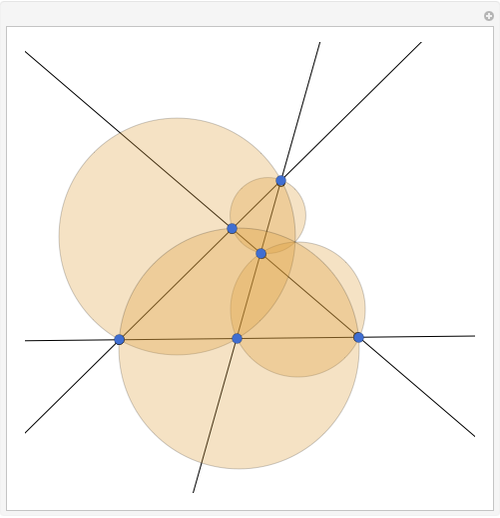
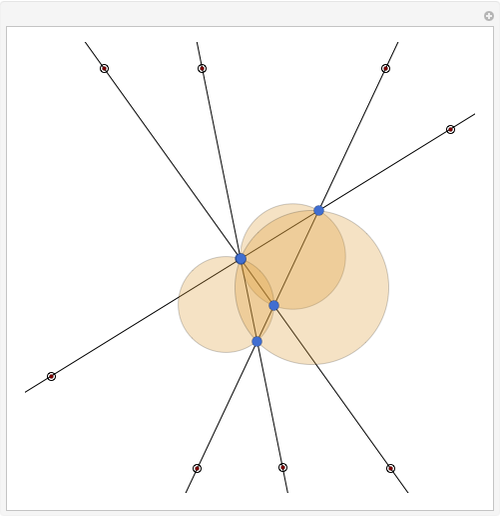
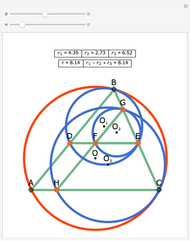
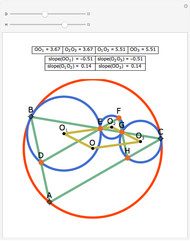
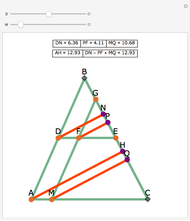
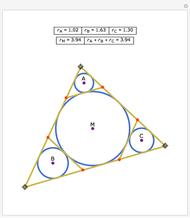
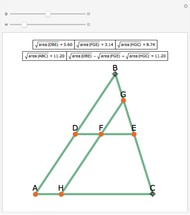
Consider four lines in the plane such that no two are parallel. They determine at most six intersection points (blue disks) and at most four triangles. (Collinear points do not determine a triangle. If they did, there could be up to 20 triangles.) This Demonstration shows that the four circles circumscribed about the four triangles pass through a common point. You can change the positions of the four lines by dragging the doubly circled locators. When will the point of intersection of the four circles lie on one or more of the four lines?