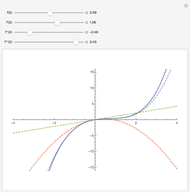
Fractional Differintegrals of Several Functions

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
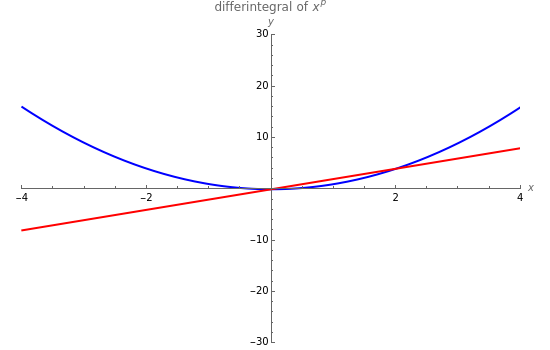
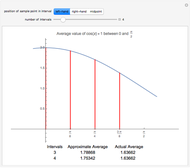
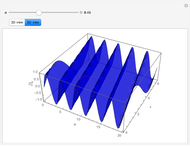
This Demonstration computes the fractional derivatives and integrals of a variety of common functions:
[more]
Contributed by: Michael Ren (March 2020)
Open content licensed under CC BY-NC-SA
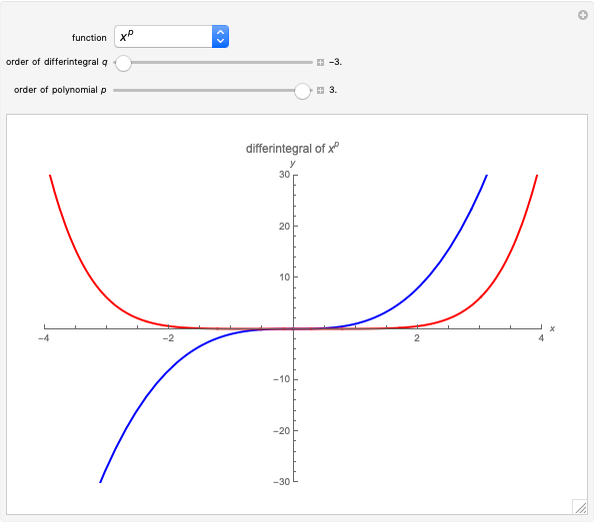
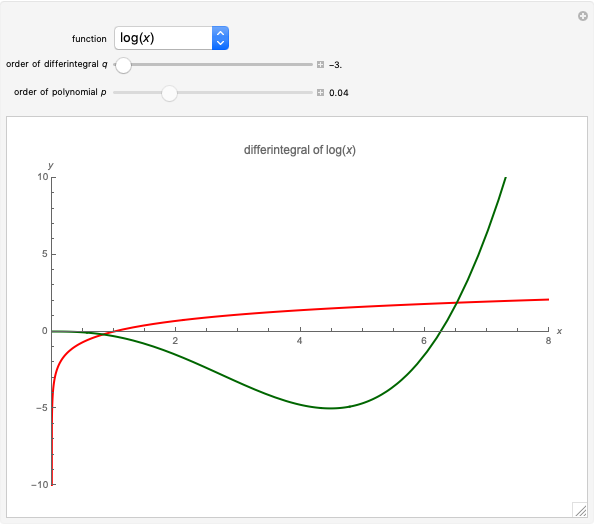
Snapshots
Details
Let  be real and
be real and  be an integrable real function of a real variable. The following is the formula for the fractional differintegral of order
be an integrable real function of a real variable. The following is the formula for the fractional differintegral of order  of
of  , using the Riemann–Liouville definition [1] with zero as the lower limit of integration:
, using the Riemann–Liouville definition [1] with zero as the lower limit of integration:

 where
where  InlineMath denotes the ordinary derivative of order
InlineMath denotes the ordinary derivative of order  , where
, where  is a positive integer.
is a positive integer.
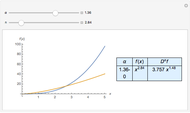
In this Demonstration, the arguments  and
and  denote the two arguments of the incomplete beta function, while
denote the two arguments of the incomplete beta function, while  usually means the order of the differintegral, and
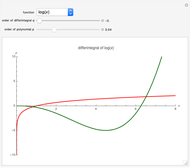
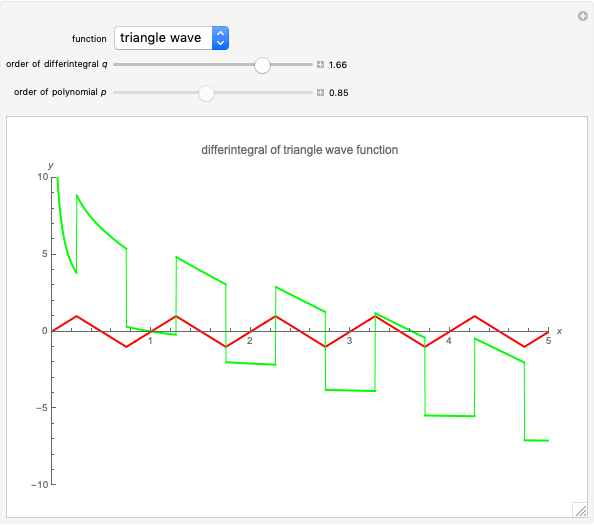
usually means the order of the differintegral, and  is the degree of a polynomial. For practical purposes, some singularities have been excluded and replaced with their ordinary derivatives; these singularities arise from the plots of the beta function for nonpositive arguments, the derivatives of integer order for the logarithmic function, and order zero for the exponential. Closed-form expressions were chosen for the differintegral to speed up plotting. For the triangle wave function, plot exclusions were introduced for visual purposes, although the derivative does not exist at these discontinuities.
is the degree of a polynomial. For practical purposes, some singularities have been excluded and replaced with their ordinary derivatives; these singularities arise from the plots of the beta function for nonpositive arguments, the derivatives of integer order for the logarithmic function, and order zero for the exponential. Closed-form expressions were chosen for the differintegral to speed up plotting. For the triangle wave function, plot exclusions were introduced for visual purposes, although the derivative does not exist at these discontinuities.
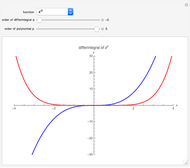
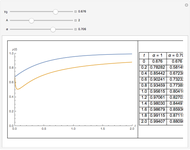
For the exponential function, the lower limit equals negative infinity. In this Demonstration, the original graph of the exponential is compared to the graph of the fractional differintegral of the exponential with  as the lower limit. For example, setting
as the lower limit. For example, setting  generates a result that deviates from the exponential function itself. This corresponds to the semi-differentiation of the exponential function, but fails to take into consideration that a fractional differintegral is, in general, nonlocal and depends on a range specific to the function. The author believes that this is very valuable in demonstrating the nonlocality of differintegration operations.
generates a result that deviates from the exponential function itself. This corresponds to the semi-differentiation of the exponential function, but fails to take into consideration that a fractional differintegral is, in general, nonlocal and depends on a range specific to the function. The author believes that this is very valuable in demonstrating the nonlocality of differintegration operations.
This was a project for Advanced Topics in Mathematics II, 2019–2020, Torrey Pines High School, San Diego, CA.
Reference
[1] K. B. Oldham and J. Spanier, The Fractional Calculus: Theory and Applications of Differentiation and Integration to Arbitrary Order, Mineola, NY: Dover Publications Inc., 2006.
Permanent Citation