Free Energy Changes in Homogeneous Nucleation

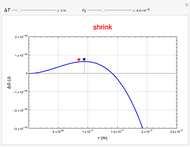
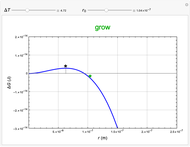
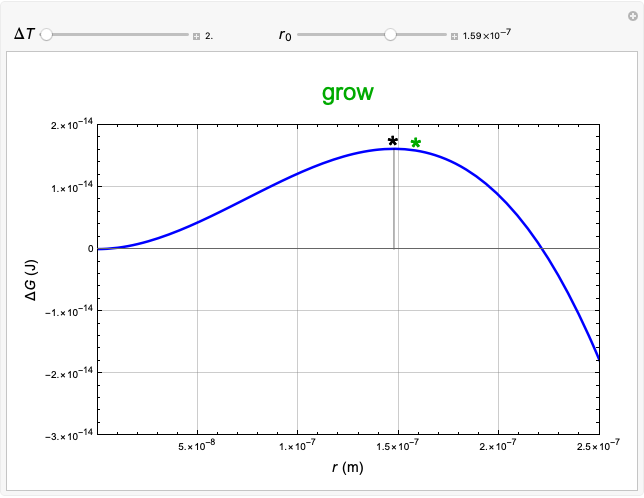
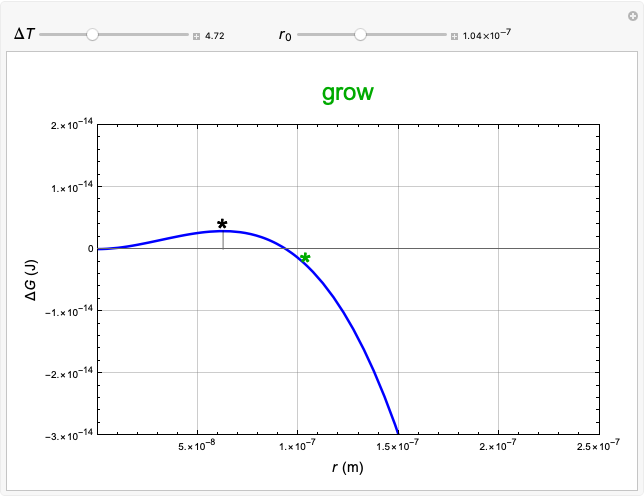
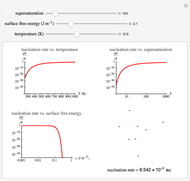
This Demonstration considers the free energy changes involved in homogeneous nucleation and growth. The plot represents the free energy of a grain (in J) as a function of the radius (in m): . As increases, the volume and surface area both increase. The interfacial term scales quadratically with the radius, while the volumetric term scales as the cube of the radius. There is no increase in free energy from interaction between like particles within a grain, thus the volumetric term decreases free energy. As the radius increases, volume increases faster than surface area, thus minimizing energetically unfavorable surface formation compared to the increase in volume.

The parameter is known as the critical radius, the point at which a grain switches from shrinking to growing. It is given by , equal to the surface energy of the solid-liquid interface divided by the volumetric change in free energy upon melting. By manipulating the change in temperature (which affects the volumetric term in both the free energy curve and the critical radius), growth or shrinkage can be determined at a given radius .

To summarize, homogeneous nucleation is governed by opposing processes in which the free energy is increased with increased surface area but decreased by the effects of nuclear radius.

The marking ★ denotes the critical radius at which the energy contribution from surface area and volume are equal and opposite.

With radii smaller than the critical radius, aggregates shrink to lower the free energy of the system.

With radii higher than the critical radius, aggregates grow to lower the free energy of the system.