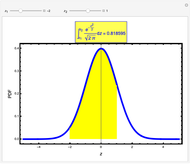
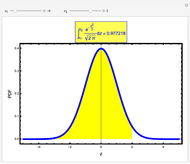
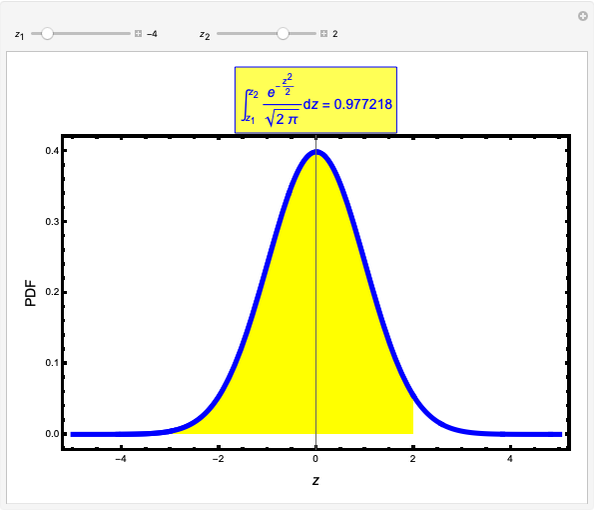
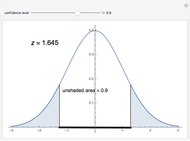
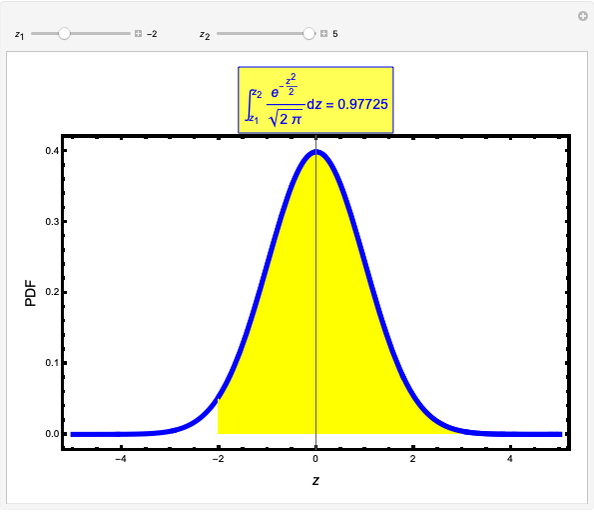
In this Demonstration, we compute integrals over the normal probability density function between two values, and . Each -score represents the number of standard deviations away from the mean, defined as , where is some value or measure, is the population mean and is the standard deviation. When integrating between two values of , the integral gives the probability or confidence interval for a measurement between these two values. For example, given a sample of tensile specimens with a population mean length of 1m and a standard deviation of 0.1m, the probability of finding a sample between 1.1m and 1.2m can be found by integrating between limits of and . This would give a probability of approximately 13.6% for finding a sample between these bounds.