Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

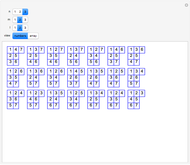
Gaussian Brackets

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

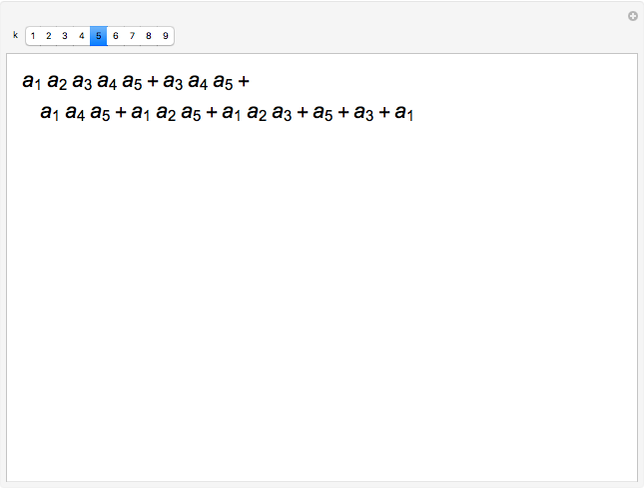
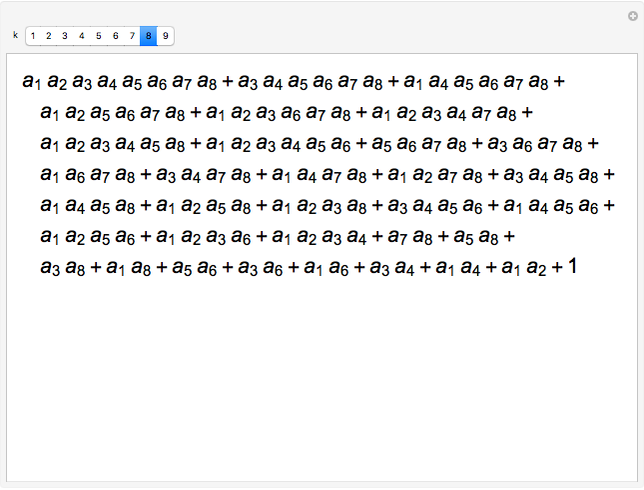
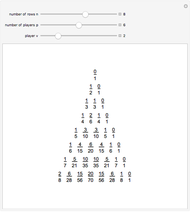
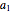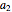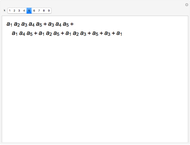
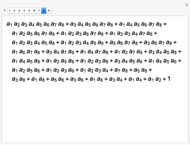
Given quantities , , …, , 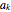the Gaussian bracket 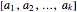is defined as the sum of all the following terms:

[more]

- the product ,

- all products that omit one pair of terms with consecutive indices,

- all products that omit two pairs of terms, each with consecutive indices,

- all products that omit three pairs of terms, each with consecutive indices,

- and so forth, where the empty product has the value 1 if is even.

[less]

Contributed by: Štefan Porubský and Szabolcs Horvát (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This term was actually introduced by Euler, who used the notation . Euler or Gauss brackets have applications in number theory, combinatorics, etc.

(The first author was supported by project 1ET200300529 of the Information Society of the National Research Program of the Czech Republic and by the Institutional Research Plan AV0Z10300504; the Demonstration was submitted 2008-04-29.)

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send