Details

Generating 3D random vectors is often required in simulations.

This Demonstration contrasts the following four methods for generating a uniform spherical 3D random vector:

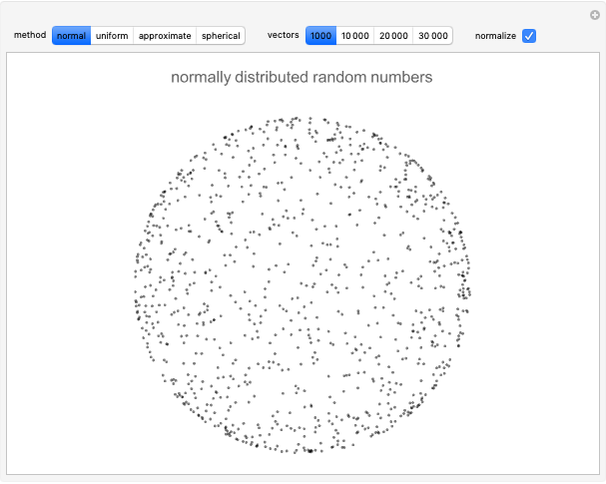
"normal" Normalize[RandomVariate[NormalDistribution[0, 1], 3]]

"uniform" Normalize[RandomReal[{-1, 1}, 3]]

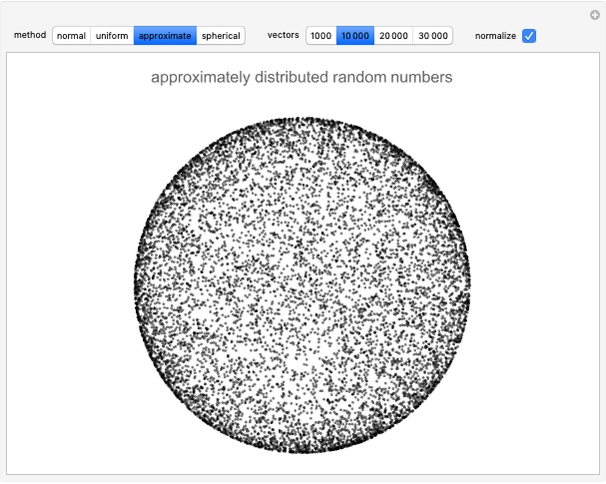
"approximate" Normalize[ArcSin[RandomReal[{-1, 1}, 3]]]

"spherical" RandomPoint[Sphere[]]

For generating 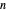uniform spherical 3D random vectors:

"normal" Normalize /@ RandomVariate[NormalDistribution[0, 1], {n, 3}]

"uniform" Normalize /@ RandomReal[{-1, 1}, {n, 3}]

"approximate" Normalize /@ ArcSin[RandomReal[{-1, 1}, {n, 3}]]

"spherical" RandomPoint[Sphere[], n]

The uniform method ends up showing clumping artifacts along the vertices and edges of a cube. Thus the Gaussian (normal) distribution is used [1]. MathWorld has an article on "Sphere Point Picking" [2] and one on "Hypersphere Point Picking" [3] describing the "normal" method.

The approximate method approximates the Normal Distribution by using Cos[x] as an approximation. If Cos[x] is a pdf (probability density function) then the cdf (cumulative distribution function) is Sin[x] and the inverse cdf is ArcSin[x]. Thus the ArcSin of a uniform random number will have an approximate Normal distribution. This seems to get rid of the clumping artifacts of the uniform method.

We eliminate the uniform method for not being uniform enough and the approximate method for being approximate. The remaining normal and spherical methods give very similar results. However, in generating a set of vectors all at once, the spherical method is 8.9 times faster, while in generating one vector at a time, the normal method is 12.7 times faster.

References

[1] D. Cross, "The Best Way to Pick a Unit Vector," Towards Data Science, Jul 19, 2020. towardsdatascience.com/the-best-way-to-pick-a-unit-vector-7bd0cc54f9b.

[2] E. W. Weisstein. "Sphere Point Picking" from Wolfram MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/SpherePointPicking (Wolfram MathWorld).

[3] E. W. Weisstein. "Hypersphere Point Picking" from Wolfram MathWorld—A Wolfram Web Resource. mathworld.wolfram.com/HyperspherePointPicking (Wolfram MathWorld).