Generating a Lemniscate IV: Rotating a Line

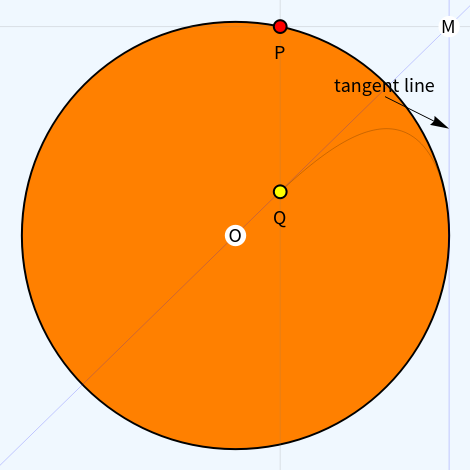
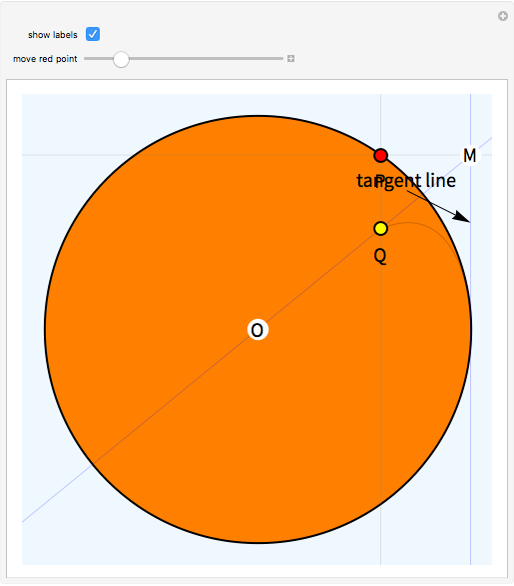
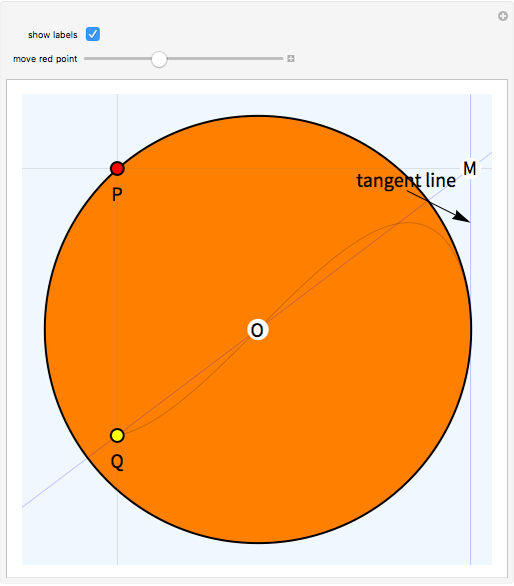
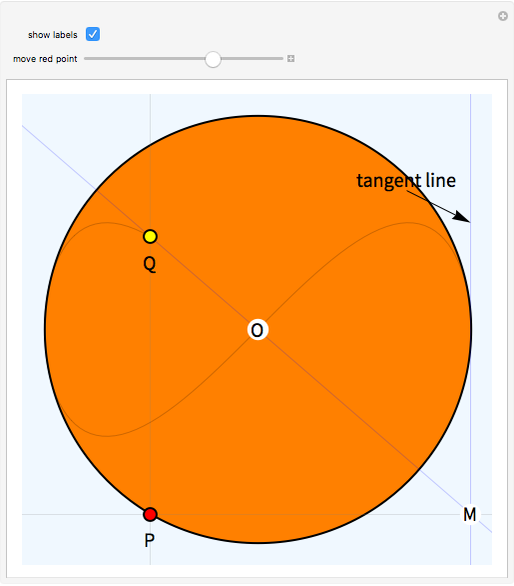
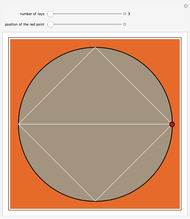
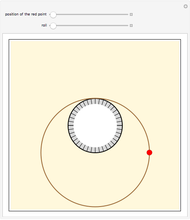
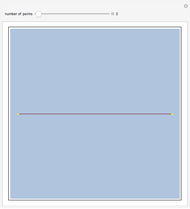
This Demonstration shows the construction of the lemniscate of Gerono. Take a circle (black with orange interior) with center O and fix one of its tangent lines (blue). Consider a point P (red) on the circle and the perpendicular to the fixed line through P intersecting at a point M. Let Q (yellow) be the intersection of line OM and a vertical line passing through P. The trace of Q as P moves on the circle is the lemniscate.