Growth in 1D Substitution Systems with Two Colors and Up to One Neighbor

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
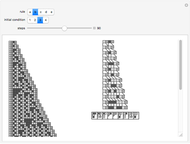
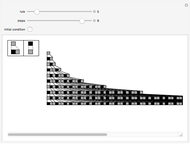
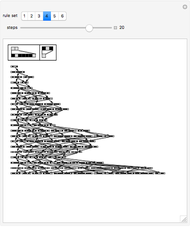
Substitution systems whose rules depend on the color of a single element and on the color of the next neighbor produce an unbalanced rate of growth and disappearance. If the rate of disappearances is too large, then almost any pattern will quickly die out, and if there are too few disappearances, then most patterns will grow exponentially or sub-exponentially. This model is a derivation of the neighbor-dependent model, allowing growth from one single cell. You can explore 117649 rules of this kind.
Contributed by: Enrique Barrajon (August 2011)
Suggested and revised by: Paul-Jean Letourneau
Open content licensed under CC BY-NC-SA
Snapshots
Details
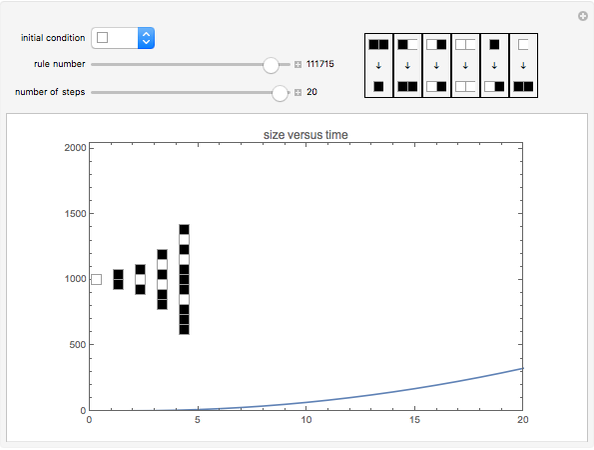
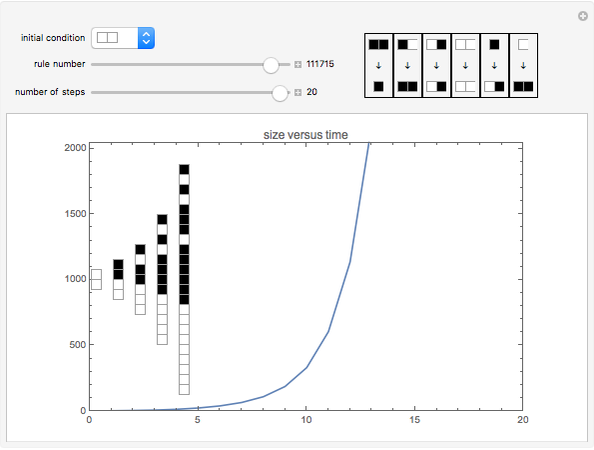
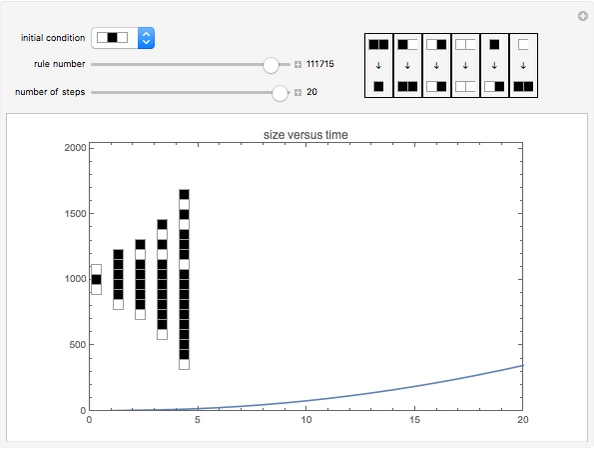
As an example, rule 111715 produces sub-exponential growth starting from a white cell. The pattern of growth is exponential when starting from two white cells, but reverts to sub-exponential when a black cell is in between them.