Heisenberg Group Action on Quintics

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
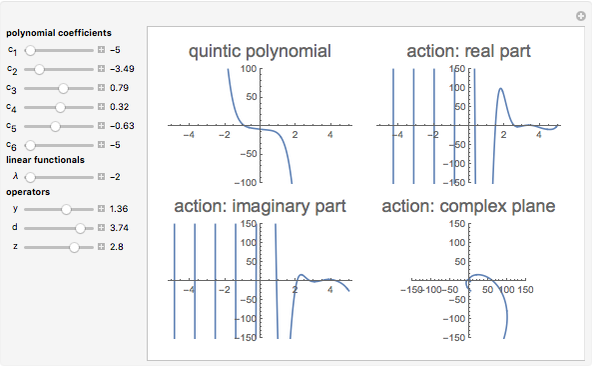
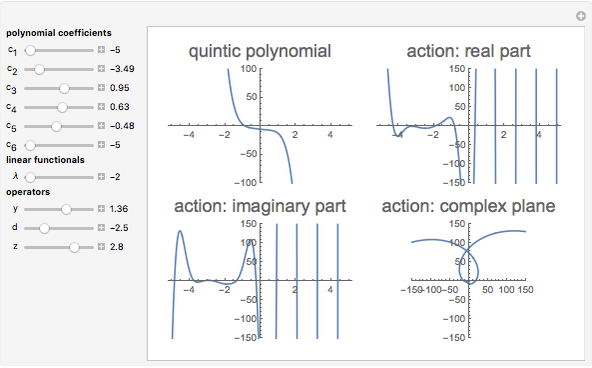
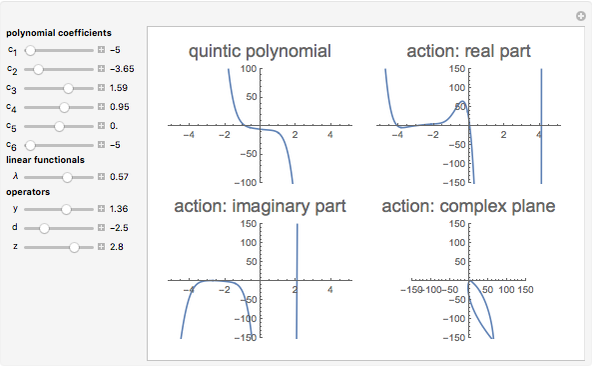
This Demonstration shows the action of the Heisenberg group on a family of quintic polynomials with compact support. The Heisenberg group is a nilpotent Lie group that has a natural action on the vector space of square integrable functions on the real line. In representation theory and quantum mechanics such actions belong to the Schrödinger representation. Let 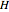 be the Heisenberg group and
be the Heisenberg group and 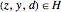 . Schrödinger representations of type
. Schrödinger representations of type  are in one-to-one correspondence with a family of linear functionals of the Lie algebra of
are in one-to-one correspondence with a family of linear functionals of the Lie algebra of  parametrized by
parametrized by 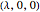 , where
, where 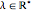 . If
. If 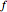 is square-integrable,
is square-integrable, 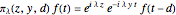 . Such actions are simply a combination of modulations and translations.
. Such actions are simply a combination of modulations and translations.
Contributed by: Vignon S. Oussa (May 2011)
(Saint Louis University)
Open content licensed under CC BY-NC-SA
Snapshots
Details
For more information on the Heisenberg group, see http://en.wikipedia.org/wiki/Heisenberg_group.
Permanent Citation
"Heisenberg Group Action on Quintics"
http://demonstrations.wolfram.com/HeisenbergGroupActionOnQuintics/
Wolfram Demonstrations Project
Published: May 23 2011