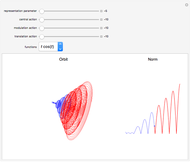
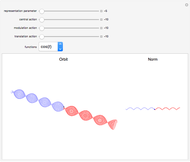
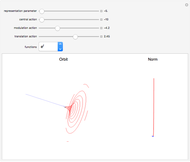
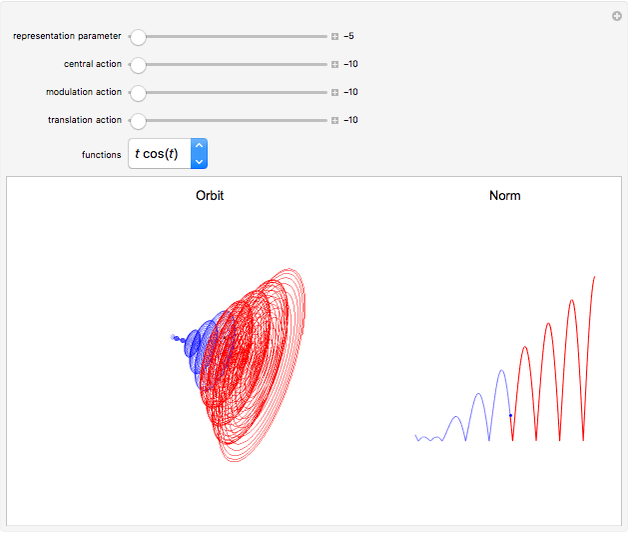
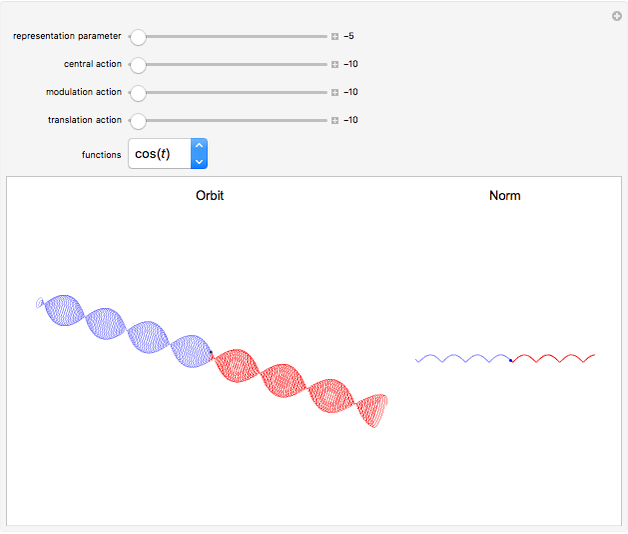
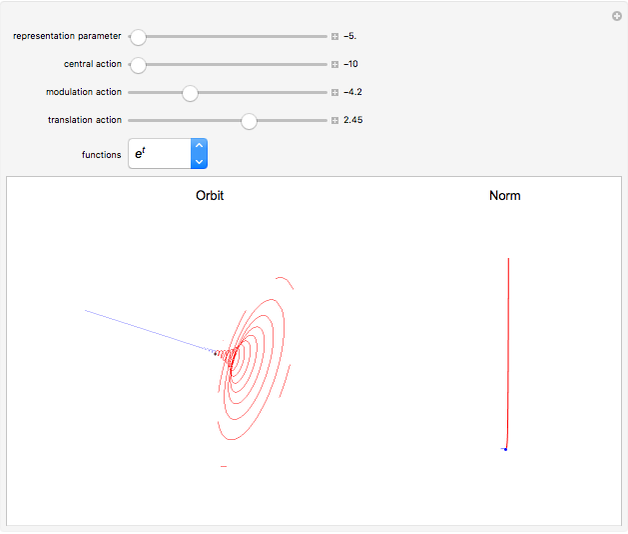
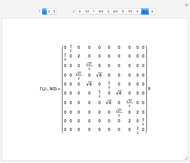
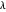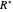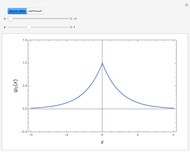
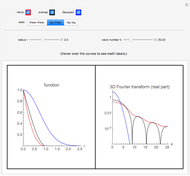
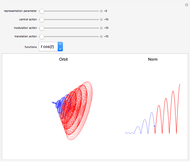
Schrödinger representations are well known in quantum mechanics, harmonic analysis, and representation theory. They are infinite-dimensional irreducible representations of the Heisenberg group. They are parametrized by linear functionals that are elements of and act on functions by multiplication of characters, modulations, and translations. This Demonstration shows how these representations act on a set of functions of compact support. The function is plotted in 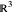on the left; on the right is the graph of the norm of the function. The central action comes from the action of the elements related to the center of the Heisenberg group acting by the multiplication of characters. The other noncentral elements are related to modulations and translation operators.