Horgan Minimal Non-Surface

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
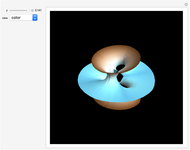
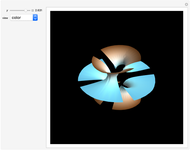
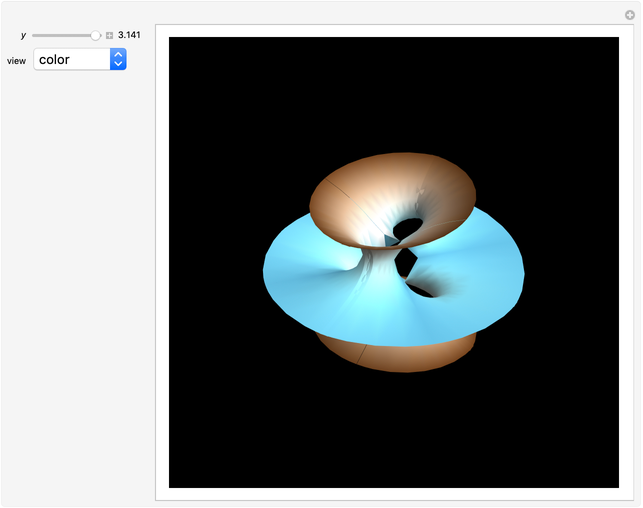
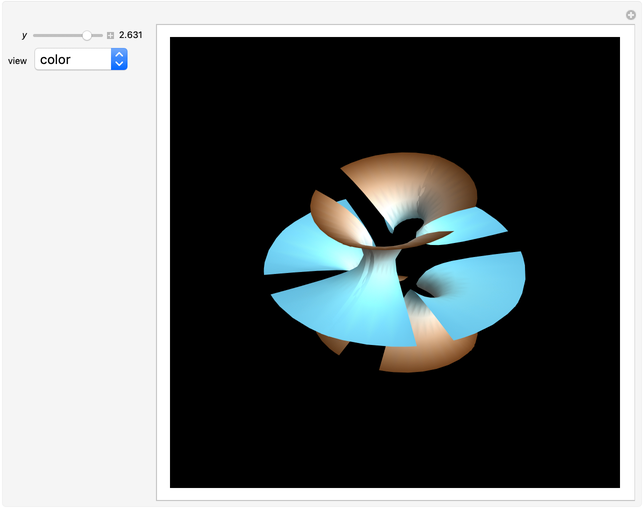
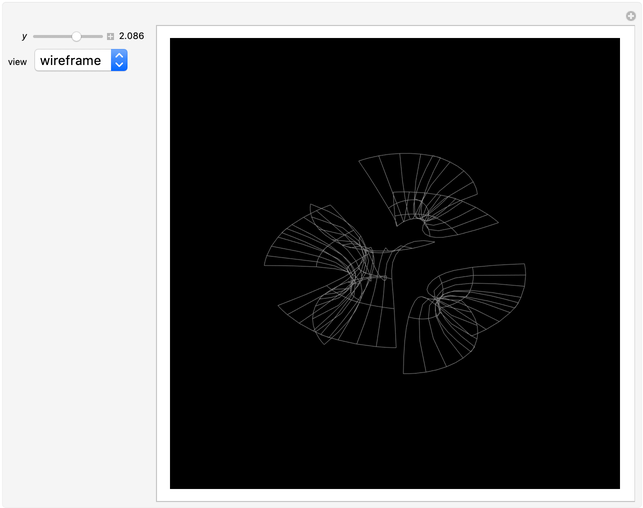
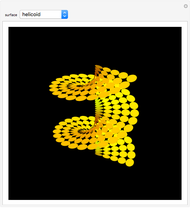
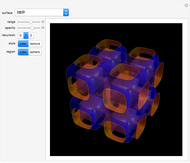
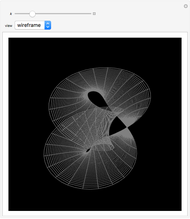
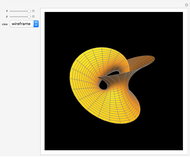
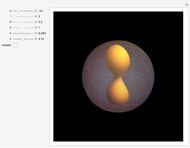
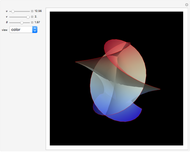
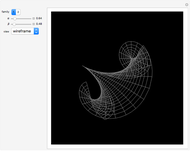
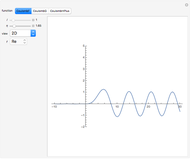
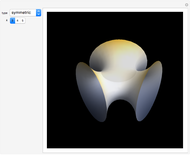
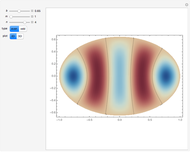
The Horgan surface is similar to the Costa minimal surface, which is an embedded surface of genus 2 with finite total curvature. (Roughly, the genus is the number of holes.) The Horgan surface can be described as the gluing of a plane with two handles at the top and the bottom, connecting to catenoid ends; but actually, it does not exist. Its existence as a surface would contradict the Hoffman–Meeks conjecture: for a complete embedded minimal surface of genus  , the number of ends must be
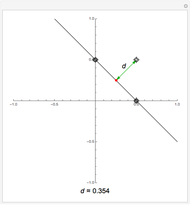
, the number of ends must be  . When the Weierstrass representation is used to solve the period problem, the periods appear in a one-parameter family and seem to be zero, but one of them becomes vanishingly small; in the limit, the resulting surface degenerates, so that the equations cannot be completely solved. For small values of the parameter
. When the Weierstrass representation is used to solve the period problem, the periods appear in a one-parameter family and seem to be zero, but one of them becomes vanishingly small; in the limit, the resulting surface degenerates, so that the equations cannot be completely solved. For small values of the parameter  , a gap can be seen, reflecting this situation.
, a gap can be seen, reflecting this situation.
Contributed by: Enrique Zeleny (January 2015)
Open content licensed under CC BY-NC-SA
Snapshots
Details
References
[1] C. J. Costa, "Example of a Complete Minimal Immersion in  of Genus One and Three-Embedded Ends," Bulletin/Brazilian Mathematical Society, 15(1–2), 1984, pp. 47–54. doi:10.1007/BF02584707.
of Genus One and Three-Embedded Ends," Bulletin/Brazilian Mathematical Society, 15(1–2), 1984, pp. 47–54. doi:10.1007/BF02584707.
[2] M. Weber, "On the Horgan Minimal Non-Surface," Calculus of Variations and Partial Differential Equations, 7(4), 1998, pp. 373–379. doi:10.1007/s005260050112.
[3] M. Weber. "The Horgan Surface." Bloomington's Virtual Minimal Surface Museum. (Dec 31, 2014) www.indiana.edu/~minimal/essays/horgan/index.html.
Permanent Citation