Hypotrochoid from Collinear Orbiters
Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
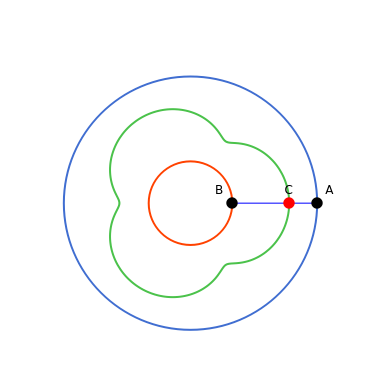
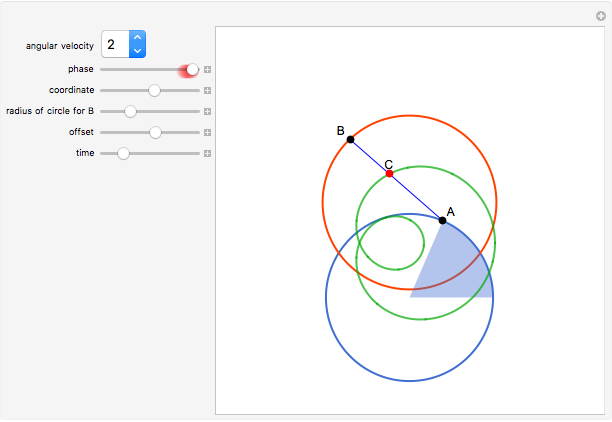
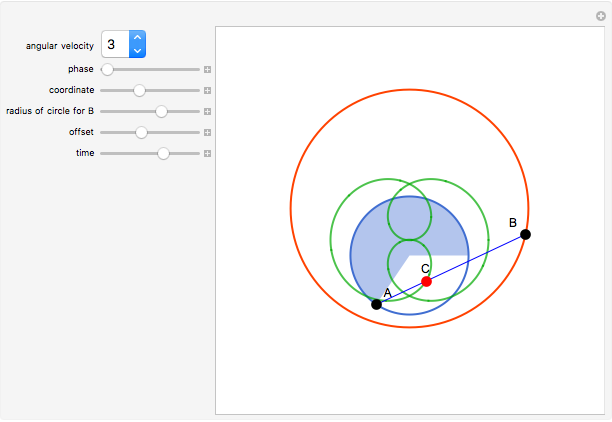
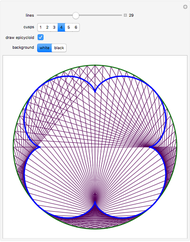
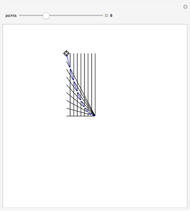
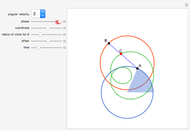
This Demonstration shows the trajectory of a red point 
on the segment 
that connects two black points 
and 
that travel around two circles. The location of is fixed in terms of the ratio 
. The phase or offset does not change the shape of the green orbit. The angular velocity of determines the number of lobes of the green curve it lies on.
Contributed by: Shenghui Yang (May 2012)
Open content licensed under CC BY-NC-SA
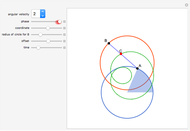
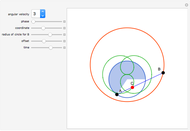
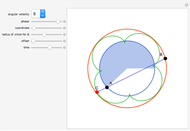
Snapshots
Details
The green figure is neither a rose curve nor a cycloid. Based on its algebraic form, it can be generated by a Spirograph with two solid gears. It is a hypotrochoid with 90 degree phase offset. Also, the inner product of the 
and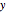 
coordinate of a point on the green curve vanishes if the angular velocity is an integer, that is, the integral of their product over one period is zero.
Permanent Citation
Spirograph
Don Piele
Rolling a Coin inside a Circle
Chris Gadzinski
Epicycloids from an Envelope of Lines
Jamie Wickham-Jones
Möbius Strip Made from a Rotating Bar
Sándor Kabai
Cyclotron 4000
Antonio Marquez-Raygoza
Cylindrical Anamorphosis of Some Popular Images
Erik Mahieu
Drawing Some Plane Curves Using Envelopes of Lines
Carine You
Doyle Spirals and Möbius Transformations
Dieter Steemann
Guilloché Patterns
Michael Schreiber
Parabolas from Rays
Michael Schreiber
