Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

1992 CMO Problem: Cocircular Orthocenters

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

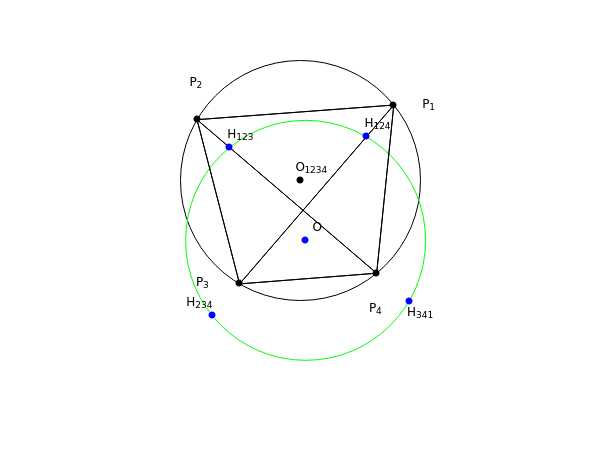
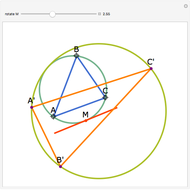
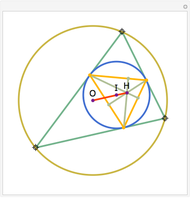
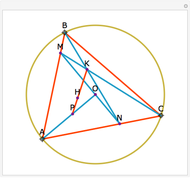
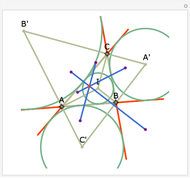
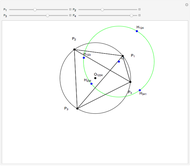
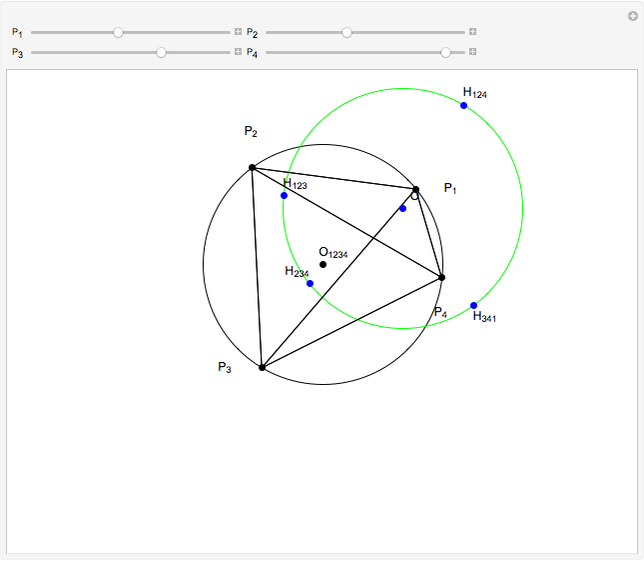
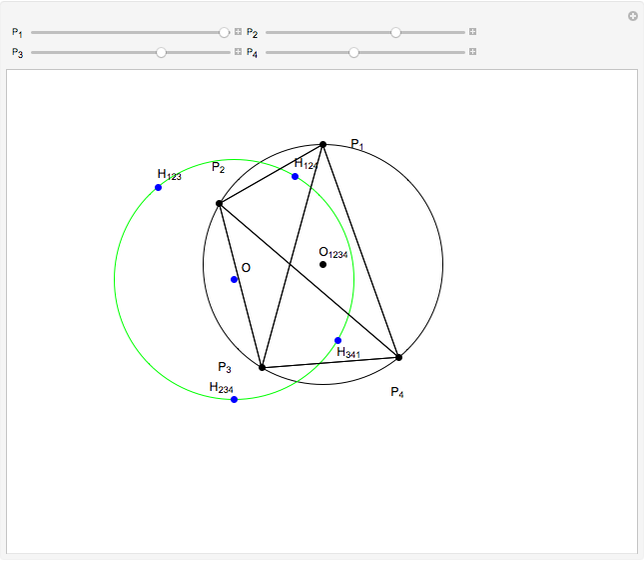
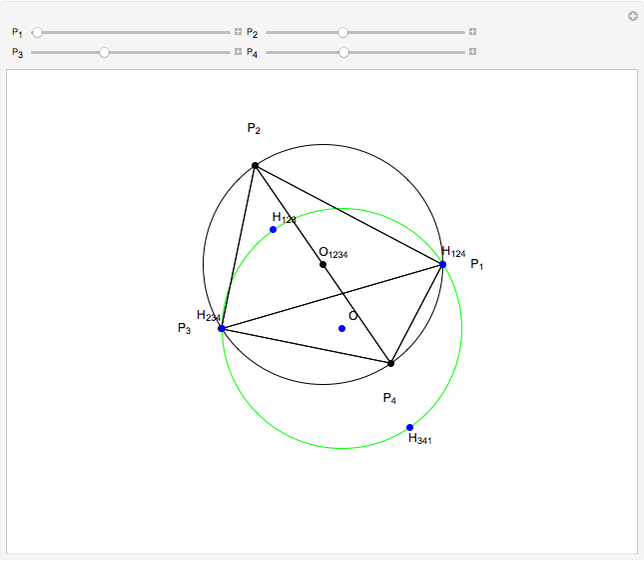
Let , , , be distinct points on a circle (black) centered at . Let be the orthocenter of triangle and so on. You can show that the four orthocenters are cocircular and the circle (green) has the same radius as the original circle.

Contributed by: Shenghui Yang (June 2012)
Open content licensed under CC BY-NC-SA

Snapshots

Details

This Demonstration is based on a problem from the 2nd Section of the Chinese Math Olympic National Final in 1992.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send