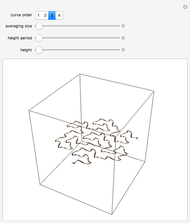
Intrinsic 3D Curves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
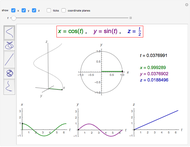
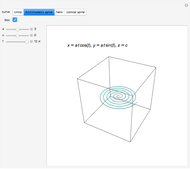
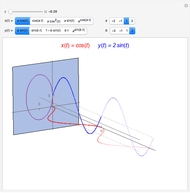
The French mathematicians Joseph Alfred Serret and Jean Frédéric Frenet found a way to represent a parametrized curve by intrinsic equations. At each point  of the curve (parametrized by arclength
of the curve (parametrized by arclength  ), three mutually perpendicular unit vectors are defined (called a TNB frame). The tangent
), three mutually perpendicular unit vectors are defined (called a TNB frame). The tangent  shows the direction of motion of the point, the normal
shows the direction of motion of the point, the normal  points toward the direction in which the curve bends, and the binormal
points toward the direction in which the curve bends, and the binormal  is a vector perpendicular to both
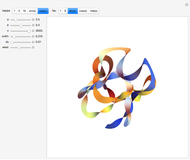
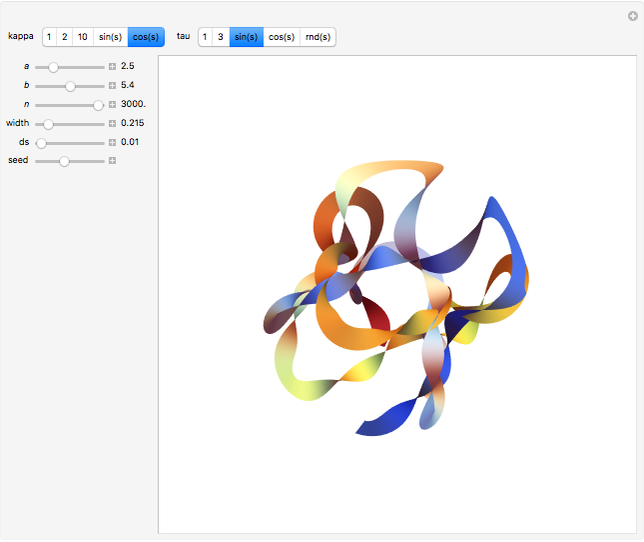
is a vector perpendicular to both . Another two quantities are introduced: curvature to measure how quickly the curve is changing its direction, and torsion to measure how quickly the curve is leaving the TN plane. In this Demonstration, the functions
. Another two quantities are introduced: curvature to measure how quickly the curve is changing its direction, and torsion to measure how quickly the curve is leaving the TN plane. In this Demonstration, the functions  (kappa, for curvature) and
(kappa, for curvature) and  (tau, for torsion) can be adjusted using the parameters
(tau, for torsion) can be adjusted using the parameters  and
and  and can be chosen to build a ribbon-like surface (in fact, a ruled surface) of a selected width and length, in discrete steps
and can be chosen to build a ribbon-like surface (in fact, a ruled surface) of a selected width and length, in discrete steps  applied
applied  times. This is possible because the other edge has the same TNB frame, but displaced.
times. This is possible because the other edge has the same TNB frame, but displaced.
Contributed by: Enrique Zeleny (December 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The Serret–Frenet equations that relate the three vectors with the curvature and torsion of a curve are
 ,
,
 ,
,
 .
.
References
[1] R. Rucker. "How Flies Fly: Kappatau Space Curves." (Dec 5, 2014) www.cs.sjsu.edu/faculty/rucker/kaptaudoc/ktpaper.htm.
[2] Wikipedia. "Frenet–Serret Formulas." (Dec 5, 2014) en.wikipedia.org/wiki/Frenet–Serret_formulas.
Permanent Citation