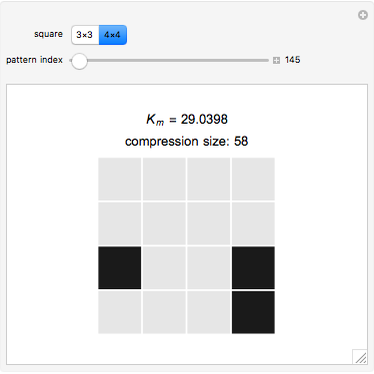
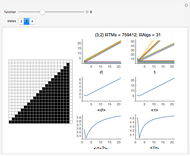
Kolmogorov Complexity of 3×3 and 4×4 Squares

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
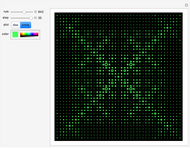
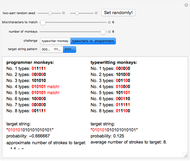
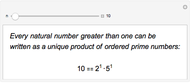
Which of "11111111111111111111", "15747363020045852837", or "81162315385411264758" can be described in the most compact way? Each can be described as it is presented, using 20 characters. The first two could be described by  and
and  . The Kolmogorov complexity
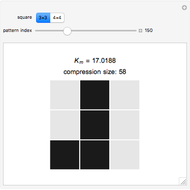
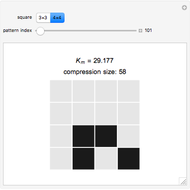
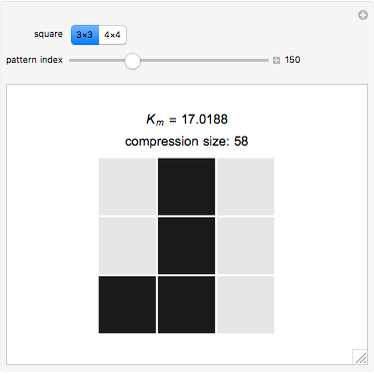
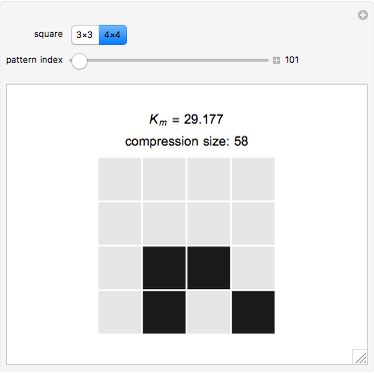
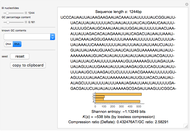
. The Kolmogorov complexity 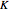 measures the length of the shortest program required to reproduce a pattern.
measures the length of the shortest program required to reproduce a pattern.
Contributed by: Fernando Soler-Toscano and Hector Zenil (February 2013)
Open content licensed under CC BY-NC-SA
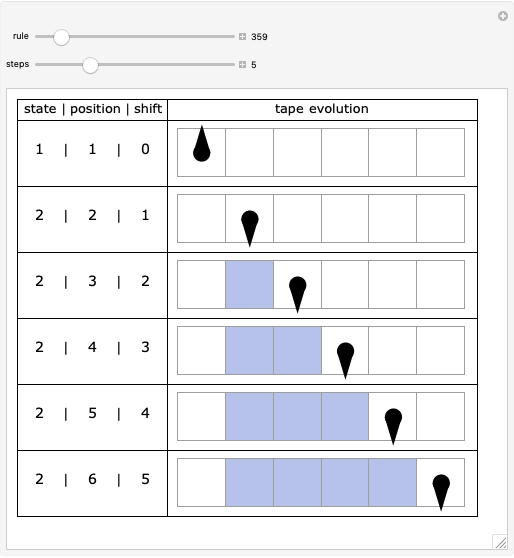
Snapshots
Details
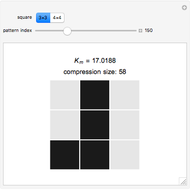
These squares are the basis of the block decomposition method [1, 2] for two-dimensional patterns used to classify the complexity of black and white bitmaps by decomposition into small squares. The block decomposition method is an extension of the coding theorem method [3, 4].
References
[1] H. Zenil, F. Soler-Toscano, J-P. Delahaye, and N. Gauvrit, "Two-Dimensional Kolmogorov Complexity and Validation of the Coding Theorem Method by Compressibility," Dec. 30, 2012. arxiv.org/abs/1212.6745.
[2] H. Zenil, F. Soler-Toscano, J-P. Delahaye, and N. Gauvrit, Evaluating Kolmogorov Complexity: An Alternative to Compression Algorithms, Heidelberg: Springer-Verlag, forthcoming.
[3] F. Soler-Toscano, H. Zenil, J-P. Delahaye, and N. Gauvrit, "Calculating Kolmogorov Complexity from the Output Frequency Distributions of Small Turing Machines," Nov. 6, 2012. arxiv.org/abs/1211.1302.
[4] The Algorithmic Nature Group. "The Online Algorithmic Complexity Calculator." (Feb 14, 2013) www.complexitycalculator.com.
Permanent Citation