Lattice Effects in Cellular Automata-Comparisons

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
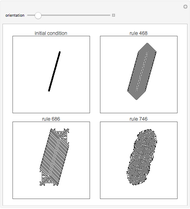
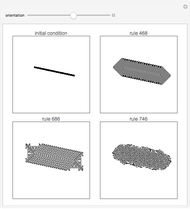
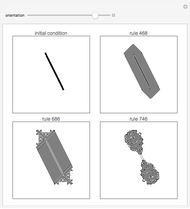
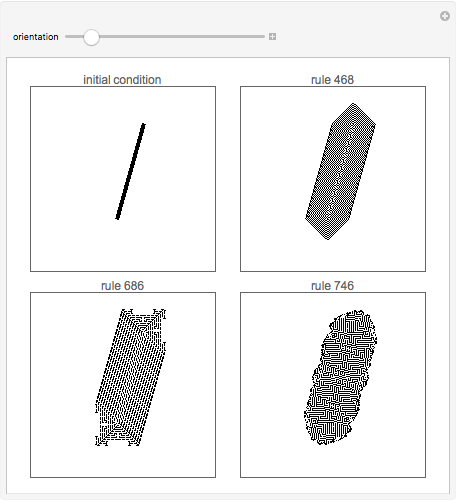
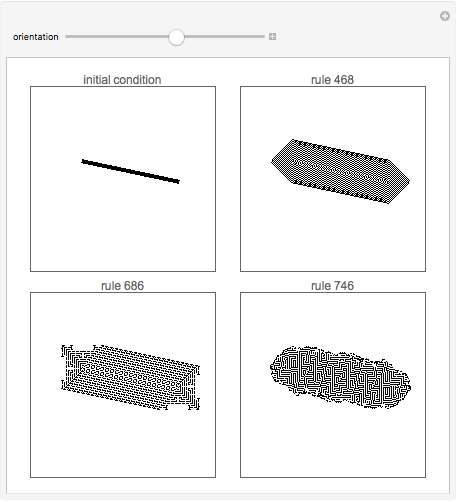
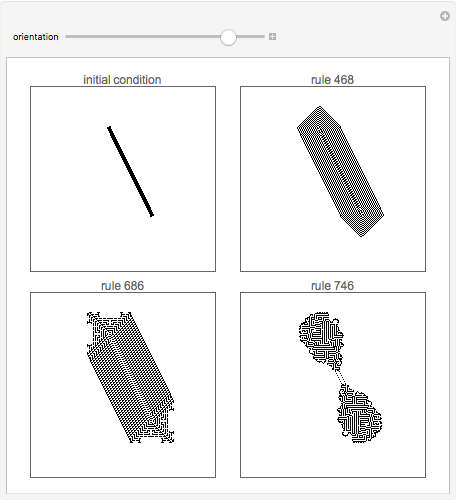
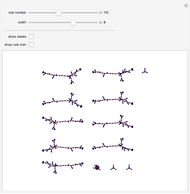
Examples of how orientation affects the behavior of two-dimensional cellular automata on a fixed grid.
Contributed by: Kovas Boguta and Fred Meinberg (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
orientation — angle of the line in the initial condition.
The arrangement of cells in cellular automata typically follows a simple, rigid structure. One-dimensional cellular automata for example are simply a sequential line of cells next to each other, while two-dimensional cellular automata most typically are arranged according to two-dimensional grids. (Hexagonal grids are also sometimes used.)
How does the fact that cellular automata typically run on regular grids affect their behavior?
With some automata, such as 4 neighbor outer totalistic code 468 and 8 neighbor outer totalistic code 686, the patterns produced always exhibit features that remain aligned with directions in the underlying grid. But with 8 neighbor outer totalistic rule 746, essentially the same rounded pattern is obtained regardless of orientation.
One consequence of behavior such as the kind that rule 746 exhibits is that we cannot rule out systems like cellular automata even when considering apparently continuous phenomena that show no obvious bias towards discrete directions.
Permanent Citation
"Lattice Effects in Cellular Automata-Comparisons"
http://demonstrations.wolfram.com/LatticeEffectsInCellularAutomataComparisons/
Wolfram Demonstrations Project
Published: March 7 2011