The Envelope Theorem: Numerical Examples

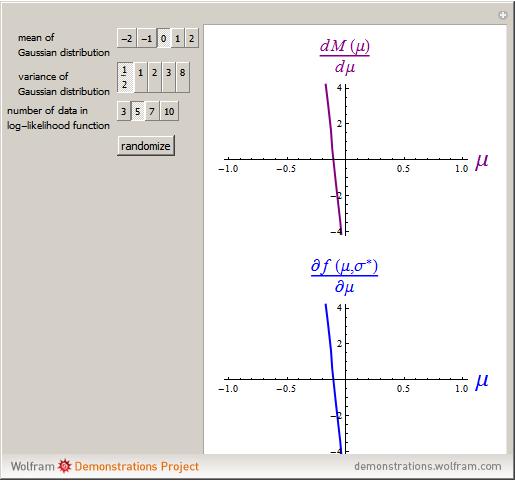
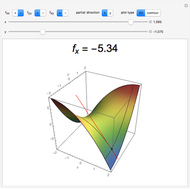
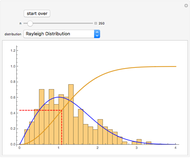
We explain the envelope theorem by way of a concrete example.

Define .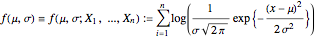

The log-likelihood maximization problem is to find parameters 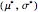such that

.

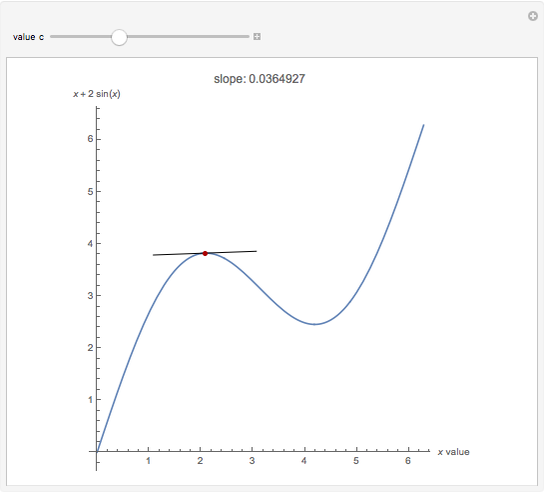
Fix and define a new function 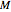such that

.

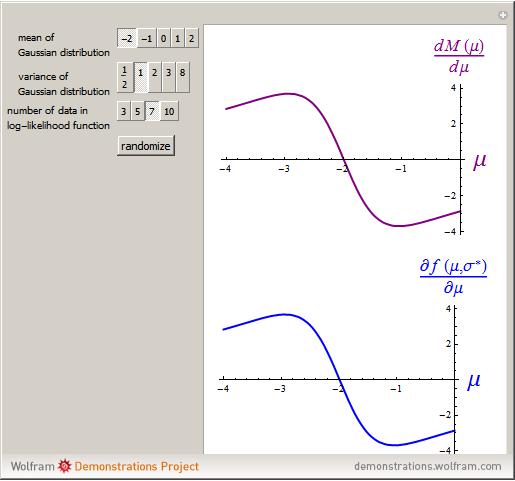
Now we view 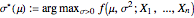. Then the envelope theorem says that

.

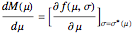The functions 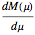and 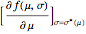are plotted in the top and bottom parts of the Demonstration output, respectively.

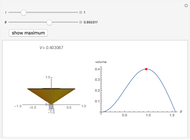
Roughly speaking, then, the envelope theorem says that fixing , maximizing over , and then taking the derivative with respect to is the same as taking the derivative with respect to , then fixing , and then substituting for the fixed the particular that maximizes.