Linear Multistep Methods for First-Order ODEs

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
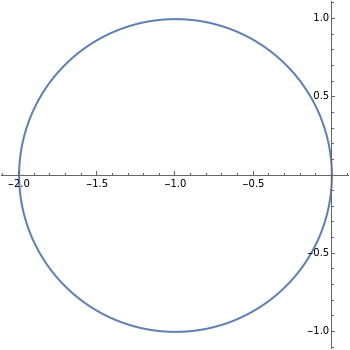
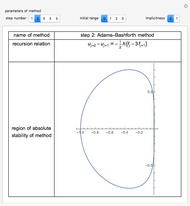
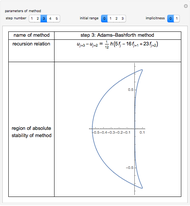
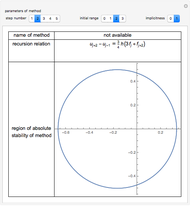
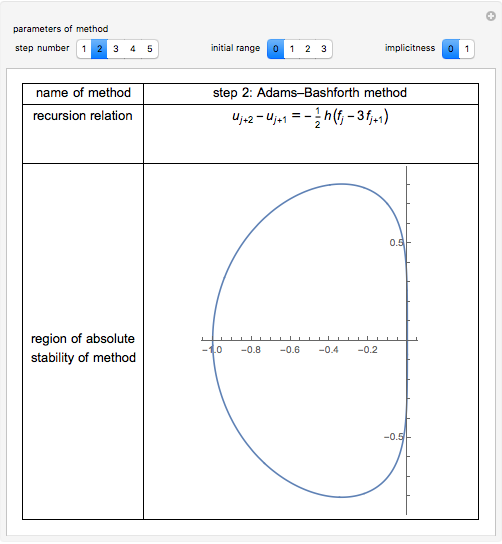
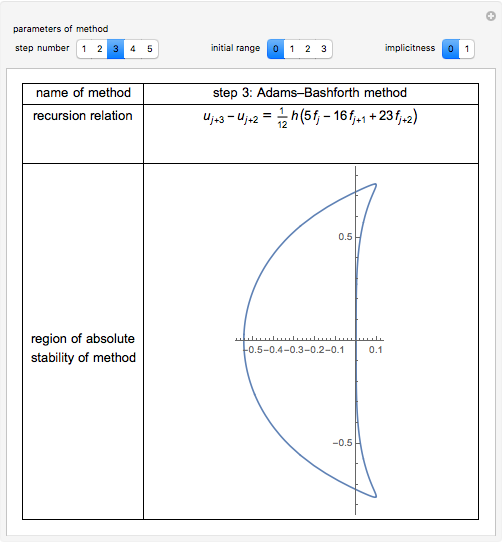
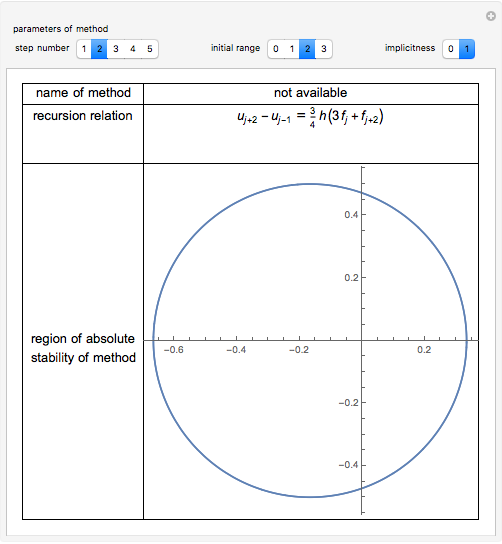
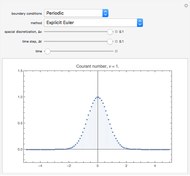
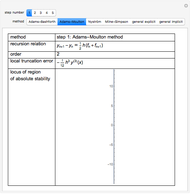
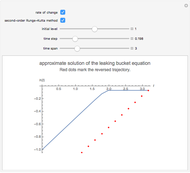
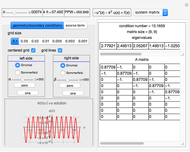
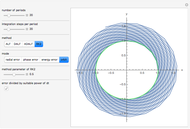
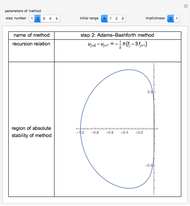
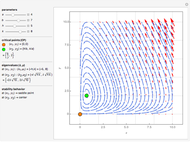
This Demonstration presents some linear multistep methods with certain parameters for solving first-order ordinary differential equations (ODEs). The name, structure and region of absolute stability of each method is shown.
Contributed by: Wusu Ashiribo Senapon and Akanbi Moses Adebowale (August 2017)
(Department of Mathematics, Lagos State University, Lagos, Nigeria)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The algorithm used in the methods presented in this Demonstration is based on the Newton backward difference interpolating polynomial. The problem  is integrated over the interval
is integrated over the interval  , and
, and  is replaced by a polynomial obtained using Newton's backward difference interpolation scheme. The regions of absolute stability of the methods are found using the locus boundary method.
is replaced by a polynomial obtained using Newton's backward difference interpolation scheme. The regions of absolute stability of the methods are found using the locus boundary method.
The control labels are described as follows:
"step number"—the step number  of the method.
of the method.
"initial range"—the value of  in the interval
in the interval  .
.
"implicitness"—the value 0 is assigned to an explicit method, while the value 1 is assigned to an implicit method.
References
[1] M. K. Jain, S. R. K. Iyengar and R. K. Jain, Numerical Methods for Scientific and Engineering Computation, 5th ed., New Delhi: New Age International, 2007.
[2] J. D. Lambert, Computational Methods in Ordinary Differential Equations, New York: John Wiley and Sons, 1973.
Permanent Citation