Logical Stochastic Resonance

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
The phenomenon of logical stochastic resonance (LSR) shows how a bistable or multistable nonlinear dynamical system can function as a logic gate or memory device by exploiting the constructive interplay of noise and nonlinearity. The response can be obtained even for subthreshold signals. The correct logical response is obtained in an optimal window of moderate noise. The functionality of the system can be switched between various gates and latch by variation of an asymmetrizing bias. The same response can be obtained with a periodic forcing such as a sinusoidal or square wave instead of noise. Furthermore, the optimal noise window can be enhanced by addition of periodic forcing so that, under low noise conditions, periodic forcing can enable the robust operation of the device.
Contributed by: Vivek Kohar (April 2014)
Based on a program by: Alejandro Luque Estepa
Open content licensed under CC BY-NC-SA
Snapshots
Details
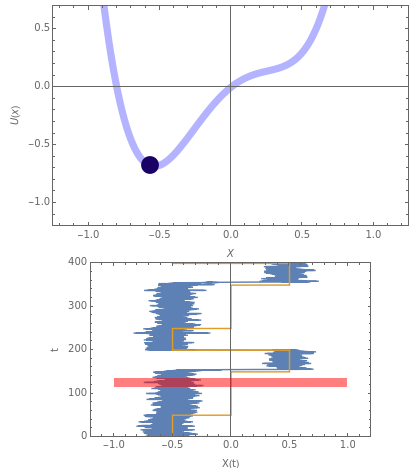
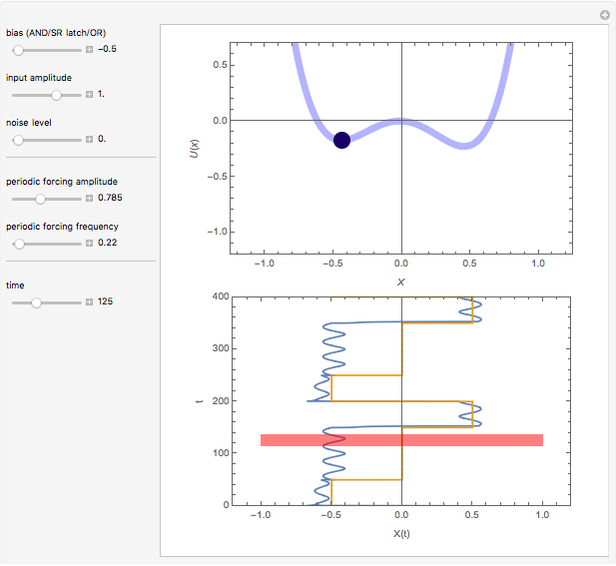
Snapshot 1: the output (blue line) does not reflect the correct logic combination of the inputs (red line) as the input strength is lower and it alone cannot drive the system in the absence of noise or periodic forcing
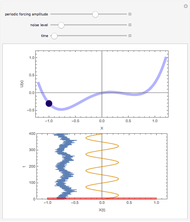
Snapshot 2: the output mimics the correct logical output in the presence of optimum noise
Snapshot 3: here noise-free LSR is shown, in which robust logic operation is obtained in the absence of noise by using only a periodic forcing (sinusoidal in this case); thus LSR can be obtained for zero or low noise
General Principle of Logical Stochastic Resonance
Consider a bistable system whose dynamical equation is given by
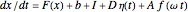 ,
,
where  is a generic nonlinear function obtained via the negative gradient of a potential with two distinct stable energy wells,
is a generic nonlinear function obtained via the negative gradient of a potential with two distinct stable energy wells, 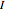 is the input signal, which is the sum of two square pulses encoding the two logic inputs,
is the input signal, which is the sum of two square pulses encoding the two logic inputs,  is the bias to asymmetrize the two potential wells,
is the bias to asymmetrize the two potential wells,  is an additive zero-mean Gaussian noise with unit variance, and
is an additive zero-mean Gaussian noise with unit variance, and 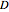 is the amplitude of noise. The functional form of the periodic forcing is
is the amplitude of noise. The functional form of the periodic forcing is 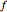 , with
, with  being the frequency and
being the frequency and 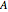 being the amplitude of the forcing.
being the amplitude of the forcing.
A logical input-output correspondence can be obtained by driving the system with two trains of aperiodic square pulses: 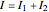 , where
, where 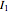 and
and 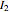 encode the two logic inputs. Logic output can be obtained from the state
encode the two logic inputs. Logic output can be obtained from the state  by defining a threshold value
by defining a threshold value 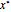 . If
. If 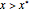 , then the logic output is interpreted to be 1, and 0 otherwise.
, then the logic output is interpreted to be 1, and 0 otherwise.
Explicit Example
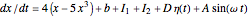
The inputs, being 0 or 1, produce four sets of binary inputs (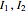 ): (0,0), (0,1), (1,0), (1,1). These four distinct input conditions give rise to three distinct values of
): (0,0), (0,1), (1,0), (1,1). These four distinct input conditions give rise to three distinct values of 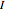 . Hence, the input signal
. Hence, the input signal 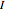 generated is a three-level aperiodic wave form. We choose 0 as our output determination threshold. If
generated is a three-level aperiodic wave form. We choose 0 as our output determination threshold. If 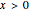 , that is, when the system is in the positive potential well, then the logic output is interpreted to be 1, and 0 otherwise. Thus the logic output toggles as the system switches wells.
, that is, when the system is in the positive potential well, then the logic output is interpreted to be 1, and 0 otherwise. Thus the logic output toggles as the system switches wells.
So a nonlinear system functioning in a noisy environment can produce a completely consistent logic gate and Set-Reset latch operation on two inputs, streaming in any random sequence. For very small or very large noise strengths, the system does not yield a reliable output. However, in a reasonably wide band of moderate noise strength, the system produces the desired output very consistently. Furthermore, the response of the system could be easily switched from memory to logic operations by varying the bias in the system. The same response can be obtained even if there is periodic forcing instead of noise, and by utilizing the constructive interplay of noise and periodic forcing it is possible to obtain a logic response similar to LSR even when the strength of noise is lower then the minimum threshold.
References
[1] K. Murali, S. Sinha, W. L. Ditto, and A. R. Bulsara, "Reliable Logic Circuit Elements that Exploit Nonlinearity in the Presence of a Noise Floor," Physical Review Letters, 102, 2009 p. 104101.
[2] V. Kohar, K. Murali, and S. Sinha, "Enhanced Logical Stochastic Resonance under Periodic Forcing," Communications in Nonlinear Science and Numerical Simulation, 19(8), 2014 pp. 2866–2873.
[3] A. Gupta, A. Sohane, V. Kohar, K. Murali, and S. Sinha, "Noise-Free Logical Stochastic Resonance," Physical Review E, 84(5), 2011 p. 055201.
[4] V. Kohar and S. Sinha, "Noise-Assisted Morphing of Memory and Logic Function," Physical Letters A, 376(8), 2012 pp. 957–962.
Permanent Citation