Filtering a White-Noise Sequence

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
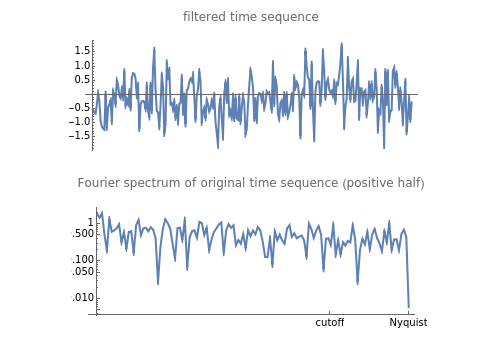
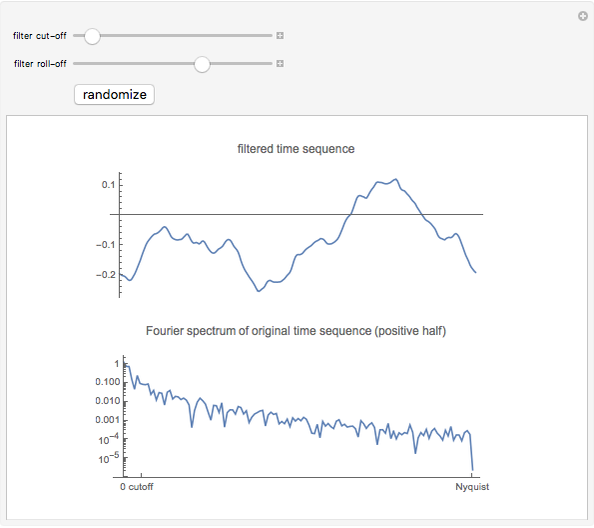
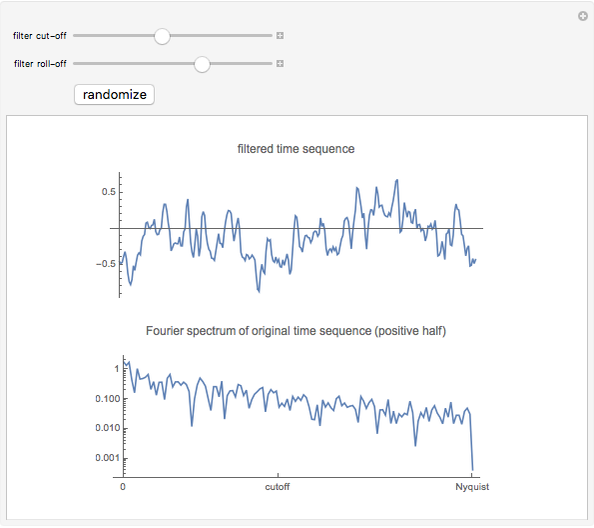
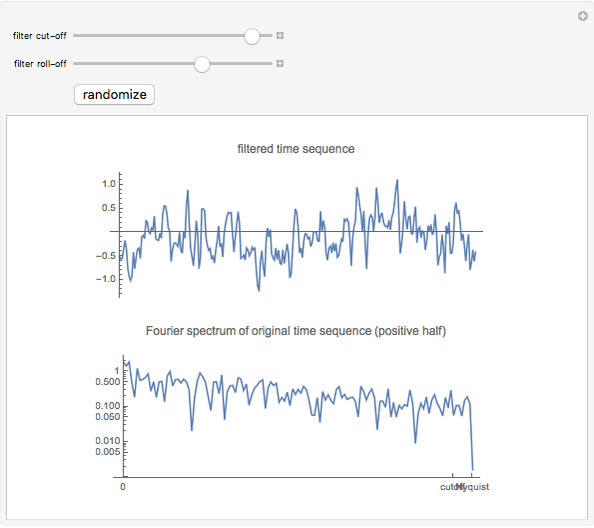
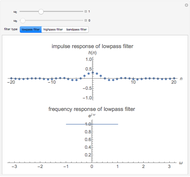
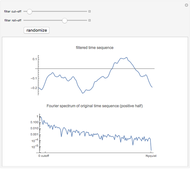
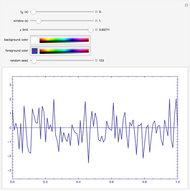
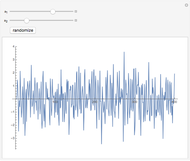
This Demonstration creates a white-noise sequence and then uses a low-pass filter to produce a red-noise sequence. The "filter cut-off" is the fractional point in [0, 1] on the spectral frequency axis to apply the filter, as measured from zero frequency. The rate of suppression of frequencies larger than the filter cut-off is given by the "filter roll-off" exponent  (1 to 4); larger values of
(1 to 4); larger values of  mean greater suppression of the higher frequencies. A new time sequence is generated with the "randomize" button. The amplitude spectrum of the time series is plotted simultaneously, with spectral values on a log scale, out to the Nyquist frequency.
mean greater suppression of the higher frequencies. A new time sequence is generated with the "randomize" button. The amplitude spectrum of the time series is plotted simultaneously, with spectral values on a log scale, out to the Nyquist frequency.
Contributed by: David von Seggern (February 2008)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The "white-noise" time sequence is created by sampling from a random normal density. To apply low-pass filtering, the sequence is converted to the frequency domain by a Fourier transform. Then the filtering factor applied to all frequencies  in the spectral domain is
in the spectral domain is
 ,
,
where  is the cut-off frequency and
is the cut-off frequency and  is the roll-off exponent. Note that the factor
is the roll-off exponent. Note that the factor  is always unity at
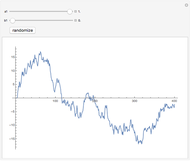
is always unity at  . The filtered Fourier spectrum is then converted back to the time domain by the inverse Fourier transform. The resultant time sequence is commonly called a "red-noise" time sequence.
. The filtered Fourier spectrum is then converted back to the time domain by the inverse Fourier transform. The resultant time sequence is commonly called a "red-noise" time sequence.
Permanent Citation