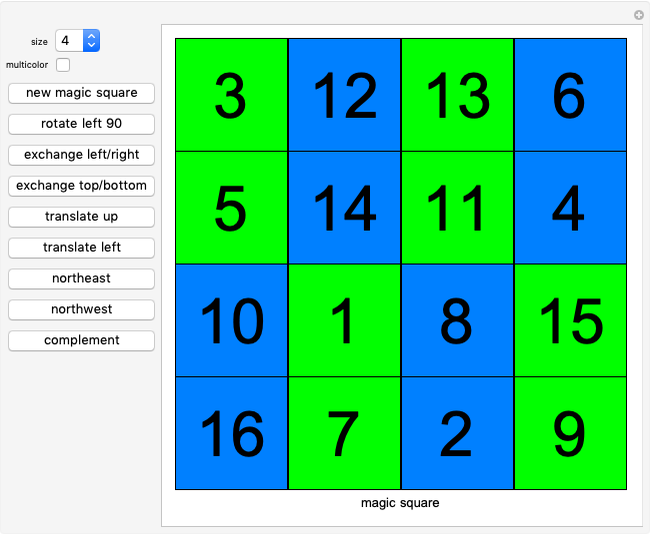
Magic Squares from Latin Squares

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
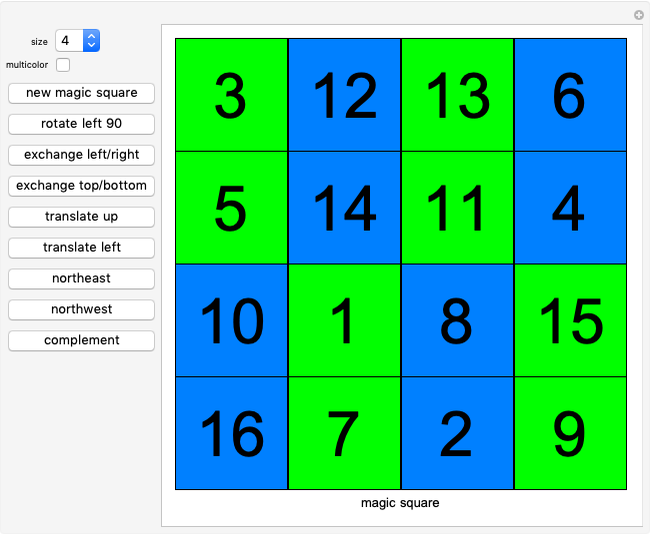
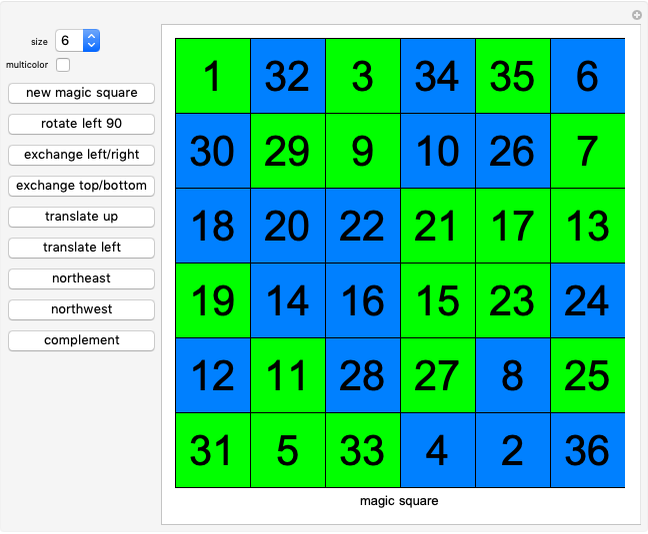
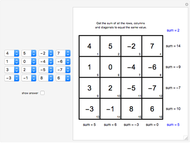
In a magic square, the rows, columns and two major diagonals have the same sum.
[more]
Contributed by: Jim Clark (July 2020)
Open content licensed under CC BY-NC-SA
Snapshots
Details
In an  Latin square (none shown in this Demonstration), all rows and columns contain one of each of
Latin square (none shown in this Demonstration), all rows and columns contain one of each of  letters, or in our case the numbers 1 to
letters, or in our case the numbers 1 to  . If the diagonals also have one of each number, the two Latin squares can be combined to form a magic square.
. If the diagonals also have one of each number, the two Latin squares can be combined to form a magic square.
This Demonstration makes magic squares from two Latin squares of positive integers using the formula  to create the magic square elements.
to create the magic square elements.
The program also makes pan magic squares. A pan magic square is a special magic square that can be shifted, rotated, reflected and complemented with the result still a pan magic square. The buttons cover a range of random-valued techniques to make random magic squares that, in most cases, are pan magic squares. The buttons "rotate left 90", "exchange left/right", "translate up", "translate left", "northeast", "northwest" and "complement" check that the resulting square is magic and therefore pan magic. This magic square construction technique was designed by John R. Hendricks and published in [1].
References
[1] J. R. Hendricks, Inlaid Magic Squares and Cubes, 2nd ed., Canada: self-published, 2000.
[2] J. R. Hendricks, Magic Squares to Tesseracts by Computer, Canada: self-published, 1998.
Permanent Citation