Wolfram Demonstrations Project

13,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

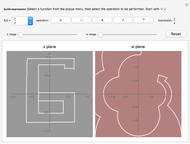
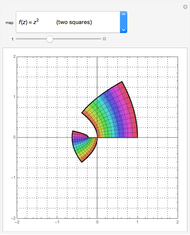
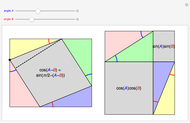
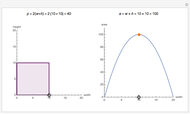
Mapping a Square by Complex Functions

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

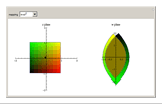
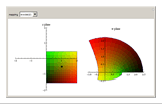
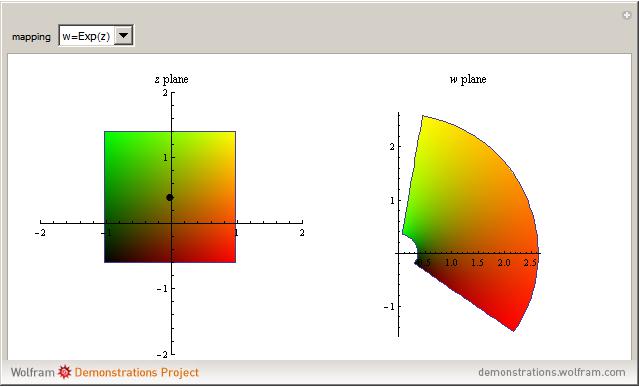
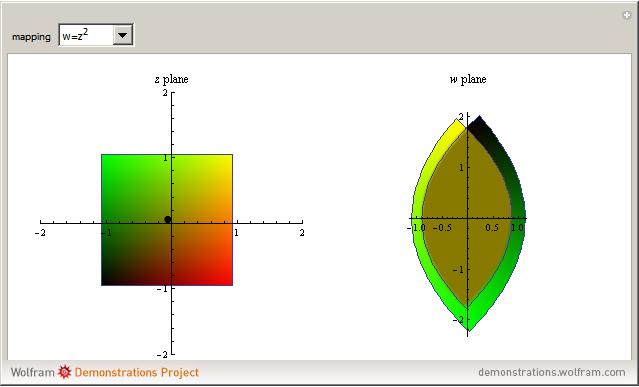
Functions of the form , where and are complex numbers, are difficult to visualize; their domains and ranges generally have two real dimensions, so the graph of the function lives in four-dimensional Euclidean space. In this Demonstration you can see how a few simple such functions transform a square of the plane.

[more]

Points in the image (right) are colored to match their pre-images (left). For functions that are not one-to-one, sometimes points in the image plane (right) are the image of more than one point in the domain square. When this happens, the color of the point in the image plane is a blend of the colors of its pre-images.

Drag the black dot on the left to move the square in the domain plane.

[less]

Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA

Snapshots

Details

detailSectionParagraph
Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send