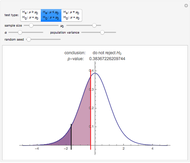
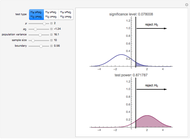
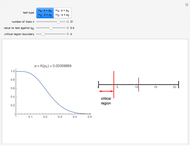
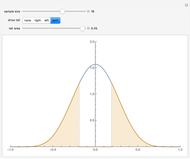
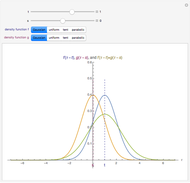
A confidence interval is a way of estimating the mean of an unknown distribution from a set of data drawn from this distribution. 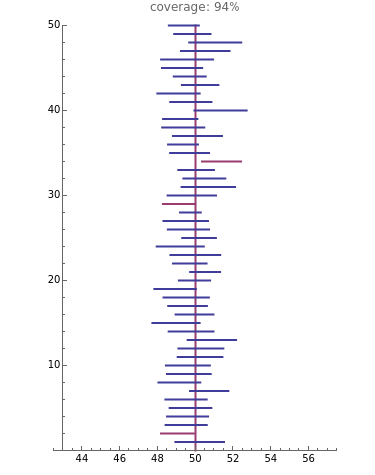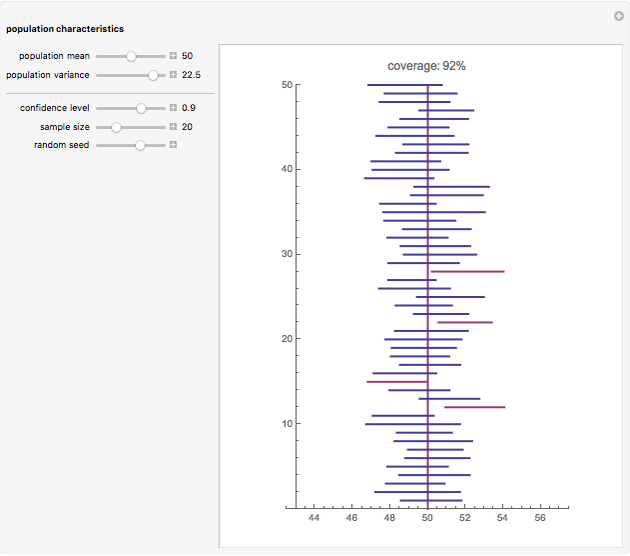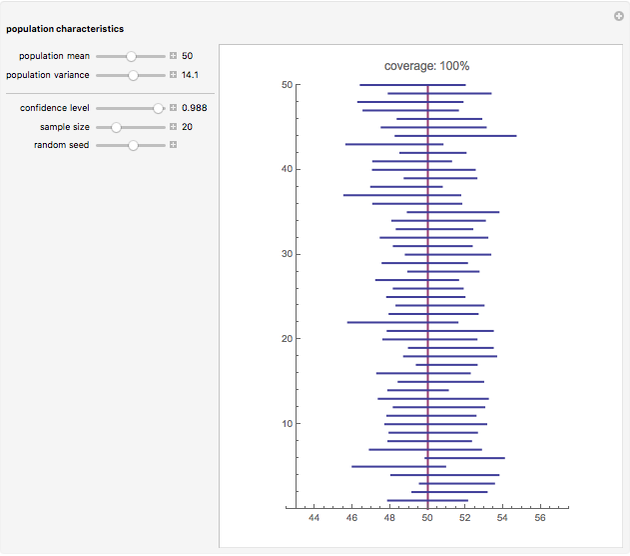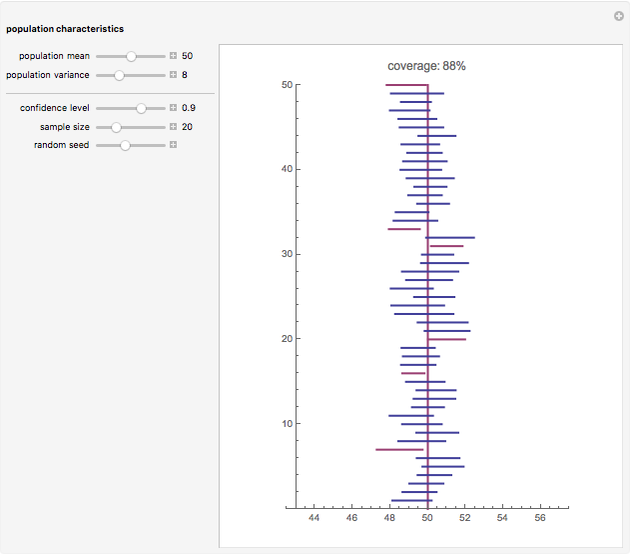If the unknown distribution is nearly normal or the sample size is sufficiently large, the interval is a confidence interval for the mean of the unknown distribution, where is the sample mean, is the quantile of the T-distribution with degrees of freedom, is the sample standard deviation, and is the sample size. If this interval were computed from repeated random samples from the unknown distribution, a fraction approaching of the time the mean of the distribution would fall in the interval. This Demonstration uses a normal distribution as the "unknown" or population distribution, whose mean and variance can be adjusted using the sliders. In the image, the vertical brown line shows the value of the mean of the "unknown" distribution, and the horizontal lines (blue if they include the true value and red if they do not) are each confidence intervals computed from different random samples from this distribution.