Minimizing the Rosenbrock Function

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
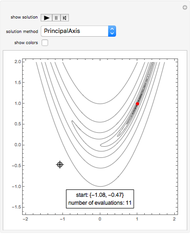
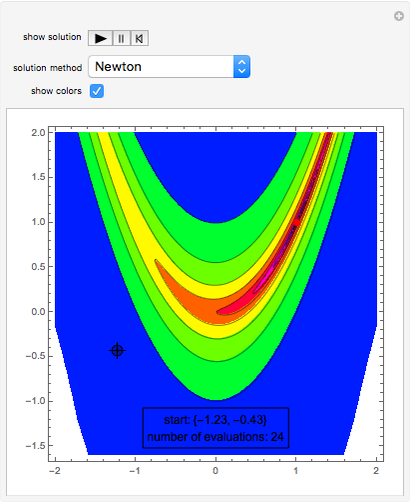
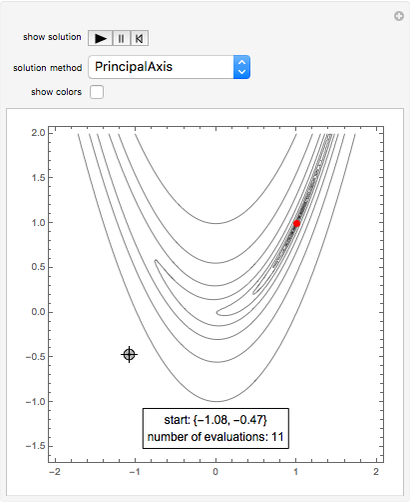
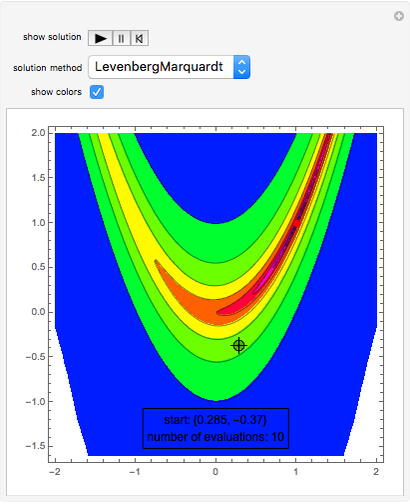
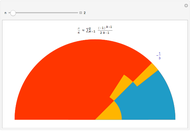
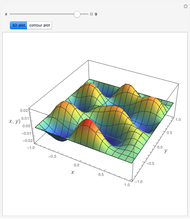
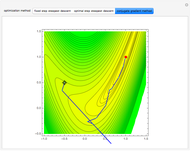
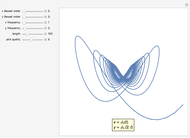
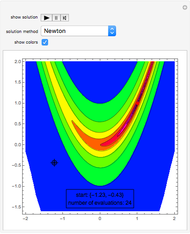
The Rosenbrock function,  , is a classic test function in optimisation theory. It is sometimes referred to as Rosenbrock's banana function due to the shape of its contour lines. The global minimum is at the point
, is a classic test function in optimisation theory. It is sometimes referred to as Rosenbrock's banana function due to the shape of its contour lines. The global minimum is at the point  that lies inside a long, narrow valley; some numerical solvers can take a long time to converge to it. In this Demonstration you can compare the performance of six different numerical methods (Conjugate Gradient, Levenberg-Marquardt, Newton, Quasi-Newton, Principal Axis and Interior Point) when they are applied to the Rosenbrock function.
that lies inside a long, narrow valley; some numerical solvers can take a long time to converge to it. In this Demonstration you can compare the performance of six different numerical methods (Conjugate Gradient, Levenberg-Marquardt, Newton, Quasi-Newton, Principal Axis and Interior Point) when they are applied to the Rosenbrock function.
Contributed by: Michael Croucher (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"Minimizing the Rosenbrock Function"
http://demonstrations.wolfram.com/MinimizingTheRosenbrockFunction/
Wolfram Demonstrations Project
Published: March 7 2011