Chebyshev Collocation Method for the Helmholtz Problem

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
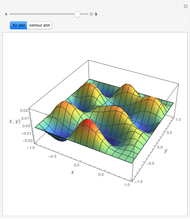
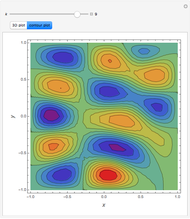
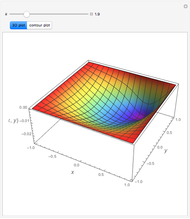
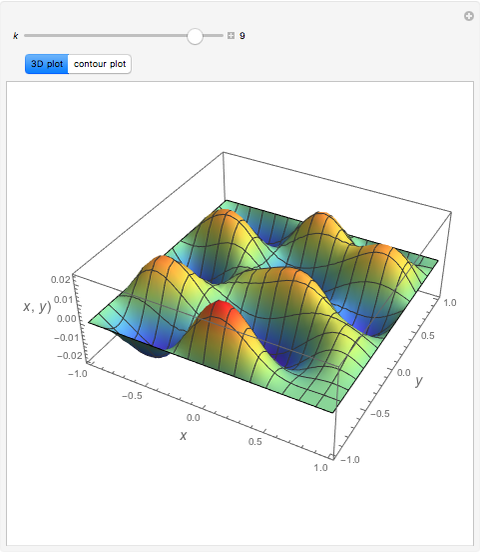
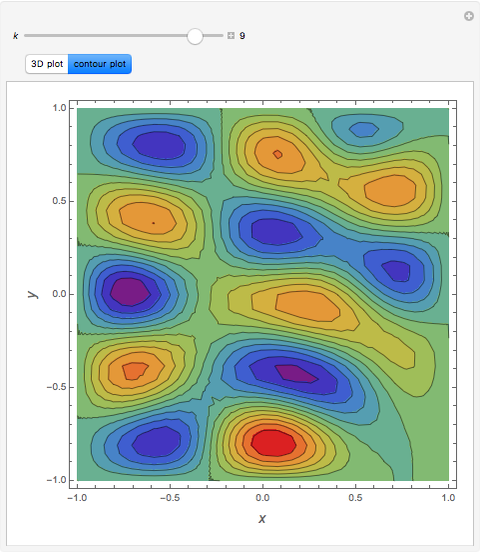
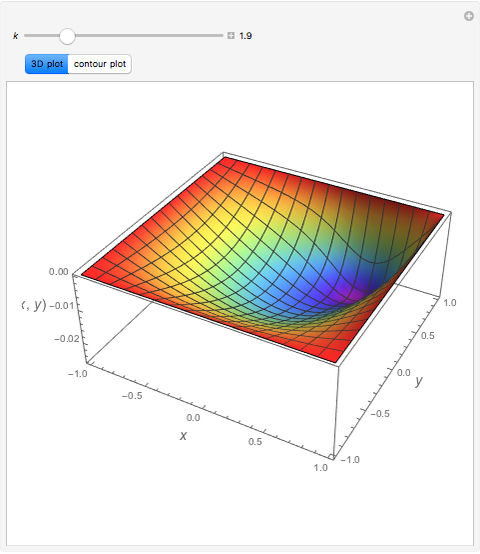
Consider the Helmholtz equation: 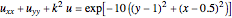 , with the boundary conditions
, with the boundary conditions  and
and  . You can set the value of
. You can set the value of  . This Demonstration then solves this PDE using the Chebyshev collocation method adapted for 2D problems. The solution is given either as a 3D plot or a contour plot.
. This Demonstration then solves this PDE using the Chebyshev collocation method adapted for 2D problems. The solution is given either as a 3D plot or a contour plot.
Contributed by: Housam Binous, Brian G. Higgins, and Ahmed Bellagi (March 2013)
Open content licensed under CC BY-NC-SA
Snapshots
Details
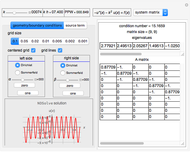
In the discrete Chebyshev–Gauss–Lobatto case, the interior points are given by  . These points are the extrema of the Chebyshev polynomials of the first kind,
. These points are the extrema of the Chebyshev polynomials of the first kind,  .
.
The  Chebyshev derivative matrix at the quadrature points is an
Chebyshev derivative matrix at the quadrature points is an  matrix
matrix  given by
given by
 ,
,  ,
,  for
for  , and
, and  for
for  and
and  ,
,
where  for
for  and
and  .
.
The discrete Laplacian is given by  where
where  is the
is the  identity matrix,
identity matrix,  is the Kronecker product operator,
is the Kronecker product operator,  , and
, and  is
is  without the first row and first column.
without the first row and first column.
Reference
[1] L. N. Trefethen, Spectral Methods in MATLAB, Philadelphia: SIAM, 2000.
Permanent Citation