Modeling Transpiration of Leaves

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
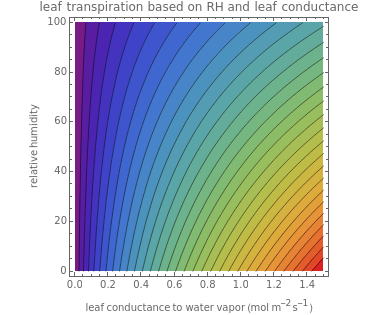
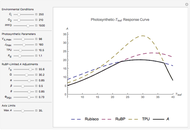
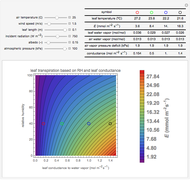
Transpiration is the transport of water vapor through plant stomatal apertures. This water loss is a necessary requirement for vascular plants as they take up carbon dioxide for photosynthesis. The two main factors that determine transpiration are the conductance of water vapor from inside the leaf to the atmosphere and the gradient of water vapor from inside to outside the leaf. It is generally assumed that the water vapor in the leaf is saturating, thus the gradient is determined by the leaf temperature and water vapor concentration in air. Here, relative humidity is used to determine the atmospheric water vapor ( axis), and leaf conductance to water vapor (
axis), and leaf conductance to water vapor ( axis) represents all diffusive conductances associated with the leaf. Transpiration is modeled based on leaf energy budget and a Fick's law analogy.
axis) represents all diffusive conductances associated with the leaf. Transpiration is modeled based on leaf energy budget and a Fick's law analogy.
Contributed by: Carl Bernacchi and Andy VanLoocke (October 2014)
Open content licensed under CC BY-NC-SA
Snapshots
Details
This Demonstration uses a leaf energy balance equation [1]:
 ,
,
where  is the leaf temperature (°C),
is the leaf temperature (°C),  is air temperature (°C),
is air temperature (°C),  is the apparent psychrometer constant (
is the apparent psychrometer constant ( ),
),  is the slope of the saturation mole fraction function (
is the slope of the saturation mole fraction function ( , with
, with  being the slope of the saturation vapor pressure function and
being the slope of the saturation vapor pressure function and  (
( ) being air pressure),
) being air pressure),  is absorbed total radiation (
is absorbed total radiation ( ),
),  is emissivity of the surface (leaf),
is emissivity of the surface (leaf),  is the Stefan–Boltzmann constant (
is the Stefan–Boltzmann constant ( ),
),  is convective-radiative conductance (
is convective-radiative conductance ( ),
),  is specific heat of air (
is specific heat of air ( ), and
), and  is vapor pressure deficit
is vapor pressure deficit  ).
).
Transpiration  (
( ) is calculated using an analogy to Fick's law:
) is calculated using an analogy to Fick's law:
 ,
,
where  , on the
, on the  axis, is leaf conductance to water vapor (
axis, is leaf conductance to water vapor ( ),
),  is saturated vapor partial pressure in the leaf based on
is saturated vapor partial pressure in the leaf based on  , and
, and  is the actual partial pressure of water vapor in air based on relative humidity, on the
is the actual partial pressure of water vapor in air based on relative humidity, on the  axis.
axis.
Reference
[1] G. S. Campbell and J. M. Norman, An Introduction to Environmental Biophysics, 2nd ed., New York: Springer, 1998.
Permanent Citation