Motion of Atoms in Crystal

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
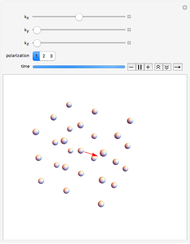
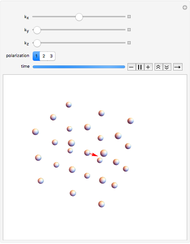
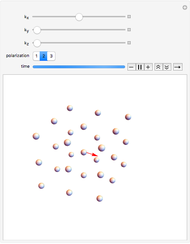
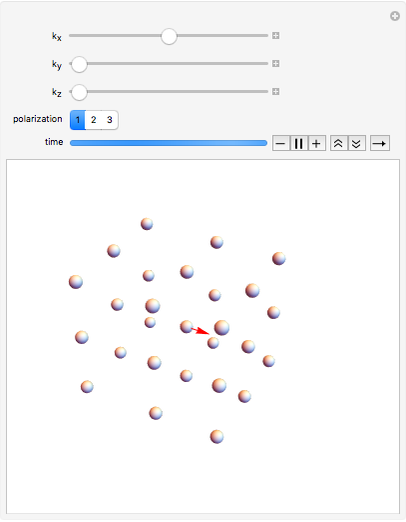
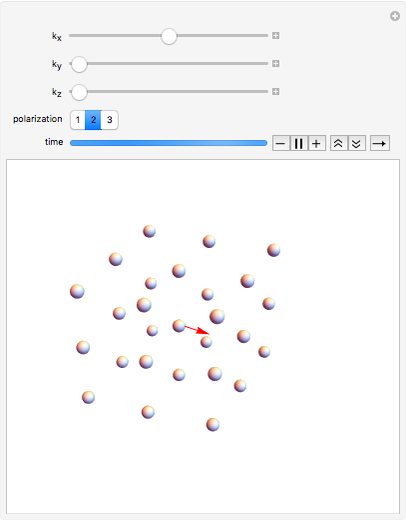
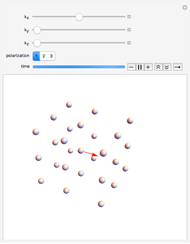
This Demonstration shows an animation of the plane-wave vibrational-mode motion of a few atoms in a simple cubic crystal. To choose vibrational mode, use the sliders to select the  vector (depicted as a red arrow) and choose the polarization, which is limited to be parallel to one of the three crystal axes. The
vector (depicted as a red arrow) and choose the polarization, which is limited to be parallel to one of the three crystal axes. The  vector specifies the direction in which the wave propagates. A longer
vector specifies the direction in which the wave propagates. A longer  corresponds to shorter wavelengths.
corresponds to shorter wavelengths.
Contributed by: T. Henighan (November 2012)
Open content licensed under CC BY-NC-SA
Snapshots
Details
The atomic motion of a classical harmonic crystal can be described as a sum of the vibrational modes, as depicted in the Demonstration. Each mode (there is a mode for every  vector) vibrates independently of the other modes, allowing one to easily calculate the ensuing motion for arbitrary of atomic displacements. You might notice modes with longer
vector) vibrates independently of the other modes, allowing one to easily calculate the ensuing motion for arbitrary of atomic displacements. You might notice modes with longer  (shorter wavelength) vibrate faster: this is generally true of simple crystals with only one atom per lattice site. In real crystals, quantum mechanics predicts that each of these vibrational modes acts as an independent quantum harmonic oscillators with quantized energy. These are called "phonon modes" and the individual quanta of energy are called "phonons". Real crystals are also not perfectly harmonic; anharmonic terms will couple the vibrational modes. However, these couplings are typically small, and the harmonic approximation is thus useful for describing the atomic motion to leading order.
(shorter wavelength) vibrate faster: this is generally true of simple crystals with only one atom per lattice site. In real crystals, quantum mechanics predicts that each of these vibrational modes acts as an independent quantum harmonic oscillators with quantized energy. These are called "phonon modes" and the individual quanta of energy are called "phonons". Real crystals are also not perfectly harmonic; anharmonic terms will couple the vibrational modes. However, these couplings are typically small, and the harmonic approximation is thus useful for describing the atomic motion to leading order.
Permanent Citation