Motion of Pendulum Interrupted by a Peg

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
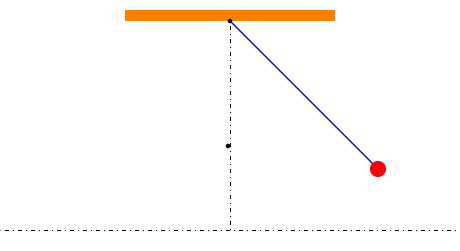
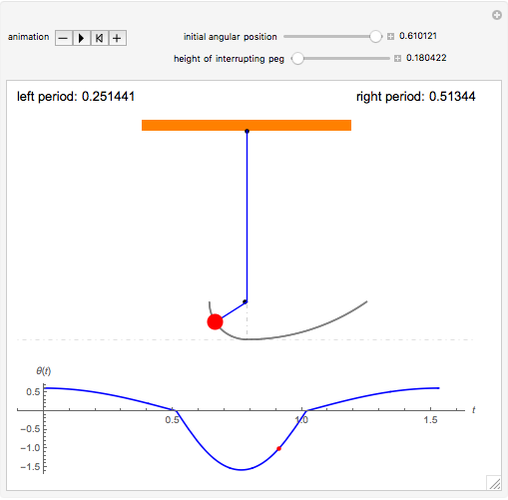
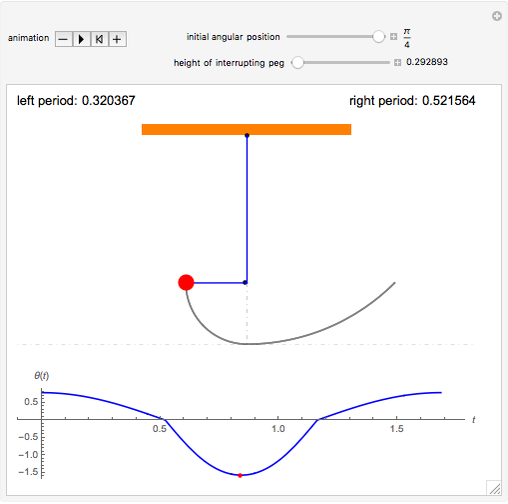
This Demonstration shows the movement of a simple pendulum whose swing is interrupted by a peg.
[more]
Contributed by: Erik Mahieu (December 2011)
Open content licensed under CC BY-NC-SA
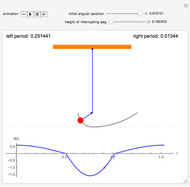
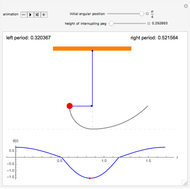
Snapshots
Details
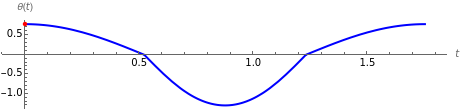
Each complete period is a sequence of four quarter-periods: two for a pendulum of length 1 and initial angle  when the bob is to the right of the vertical and two for a pendulum of length
when the bob is to the right of the vertical and two for a pendulum of length  and initial angle
and initial angle  when the bob is to the left. The quarter-periods are determined by solving the appropriate ODE and escaping the solution using Mathematica's built-in "EventLocator" method.
when the bob is to the left. The quarter-periods are determined by solving the appropriate ODE and escaping the solution using Mathematica's built-in "EventLocator" method.
An interesting article on the subject is C. E. Mungan. "Maximum Bob Height of an Interrupted Pendulum." United States Naval Academy Physics Department. (2006) usna.edu/Users/physics/mungan/_files/documents/Scholarship/InterruptedPendulum.pdf.
See also the Demonstration by Enrique Zeleney, "Interrupted Pendulum".
Permanent Citation