Normal Lines to a Parabola

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
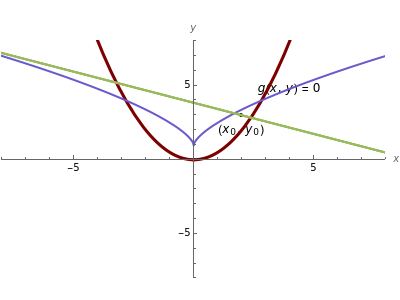
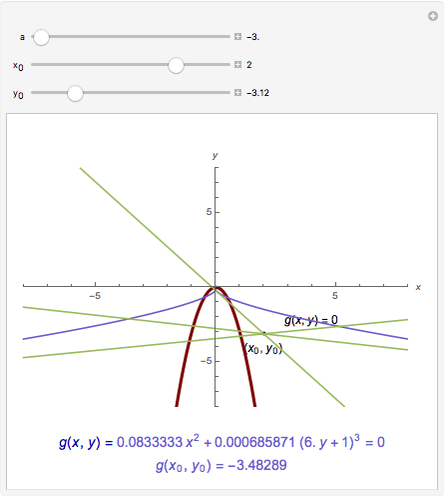
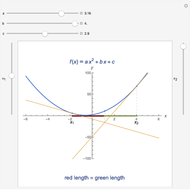
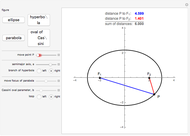
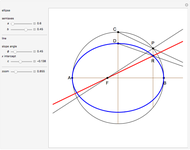
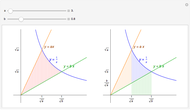
The normal line to the graph of parabola  at the point
at the point 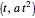 ,
, 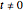 is
is 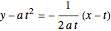 , or equivalently
, or equivalently 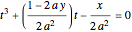 . The number of real roots of a reduced cubic
. The number of real roots of a reduced cubic 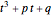 depends on the sign of
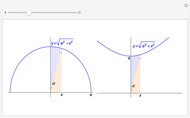
depends on the sign of  . So the number of normal lines to
. So the number of normal lines to  through
through  depends on the sign of
depends on the sign of 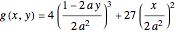 . If
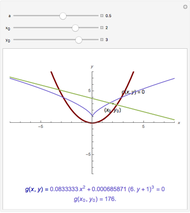
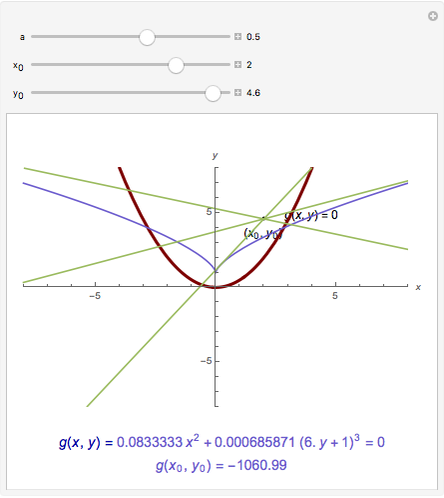
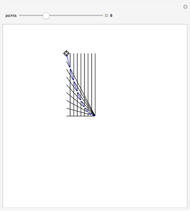
. If 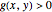 , there is one normal line to
, there is one normal line to 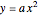 through
through 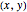 ; if
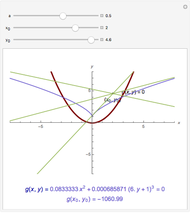
; if 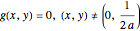 , there are two normal lines; and if
, there are two normal lines; and if 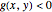 , there are three. (For the cusp
, there are three. (For the cusp 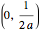 , the only normal line is
, the only normal line is  .)
.)
Contributed by: Soledad Mª Sáez Martínez and Félix Martínez de la Rosa (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
Reference: D. Sanchez and K. C. Smith, "Normal Lines and the Evolute Curve," The College Mathematics Journal, 31(5), 2000 pp. 397–403.
Permanent Citation
"Normal Lines to a Parabola"
http://demonstrations.wolfram.com/NormalLinesToAParabola/
Wolfram Demonstrations Project
Published: March 7 2011