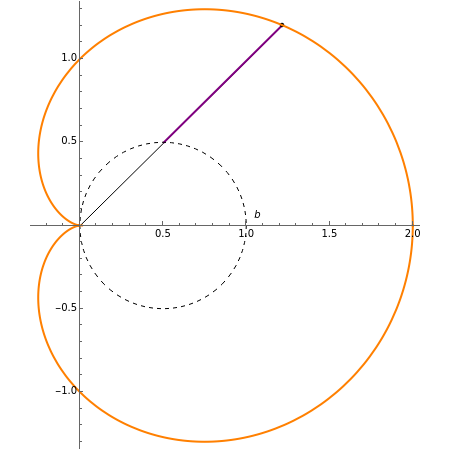
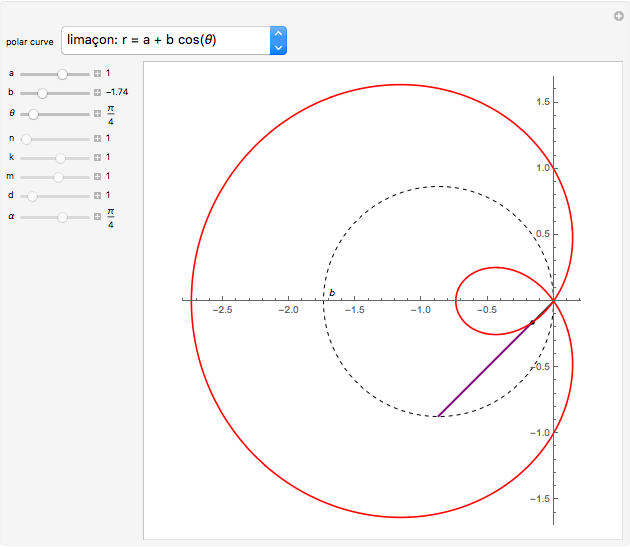
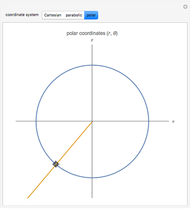
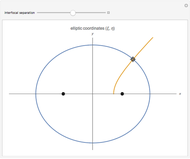
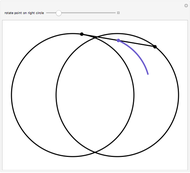
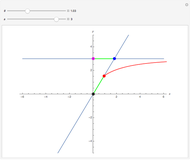
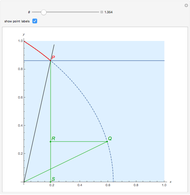
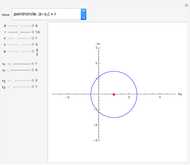
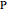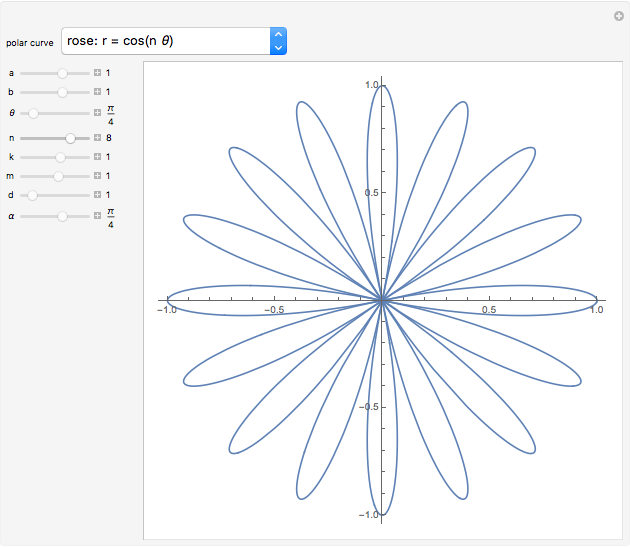
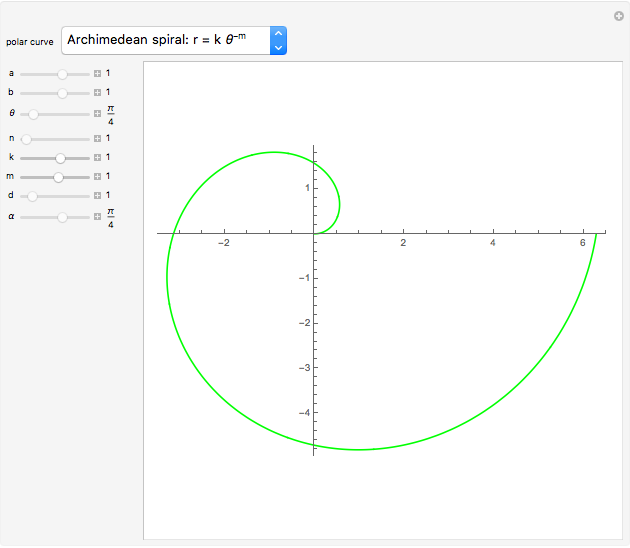
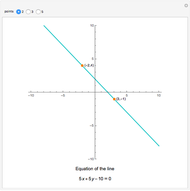
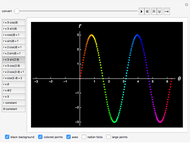
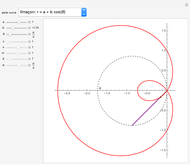
A limaçon is the locus of a point that lies on a variable line (obtained by varying the angle ) passing through a fixed point (the pole, taken to be the origin) on a circle with radius (shown dashed); is a fixed distance (shown with a purple line) from the other point of intersection of the line with the circle. By varying and , various types of limaçons are obtained, namely the circle, trisectrix, cardioid, limaçon with inner loop, dimpled limaçon, and oval (convex) limaçon. In addition, other popular plane curves (roses, spirals, lines, and lemniscates) with their polar equations are shown.