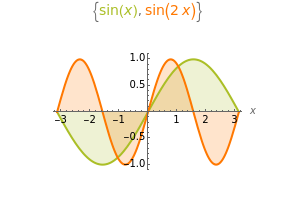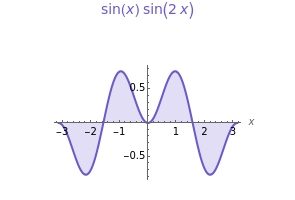
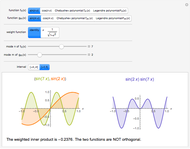
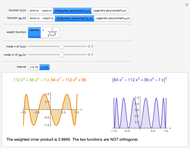
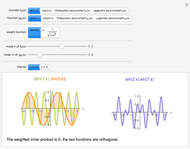
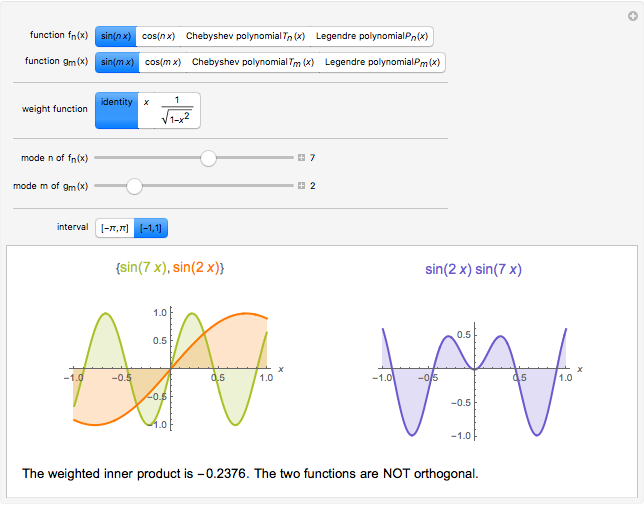
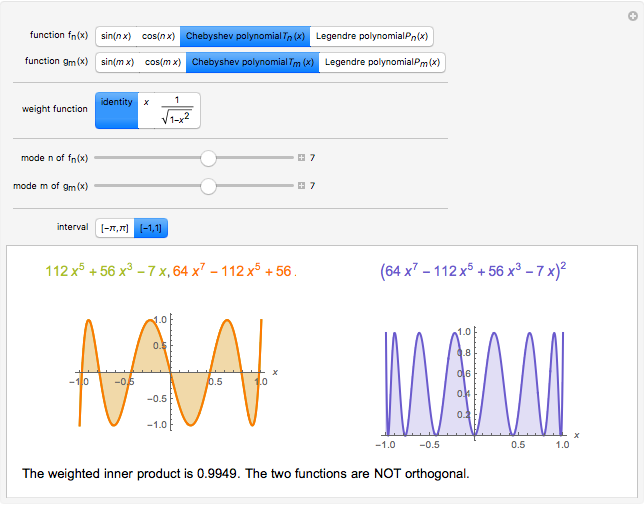
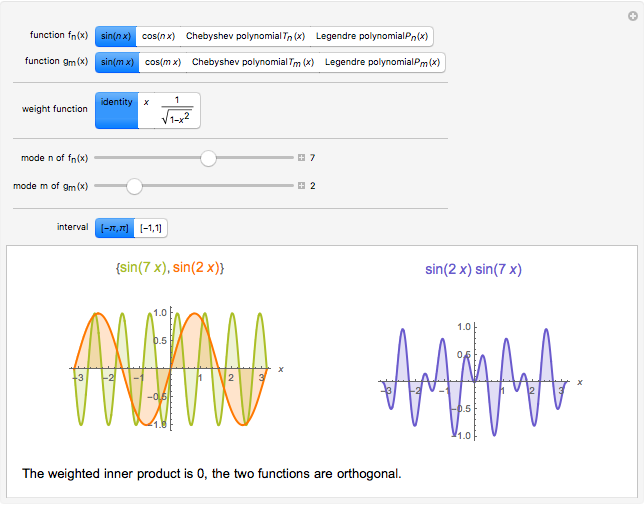
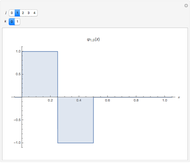
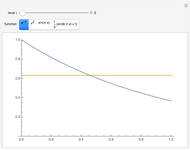
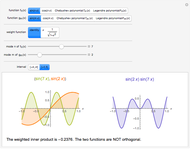
Two functions are orthogonal with respect to a weighted inner product if the integral of the product of the two functions and the weight function is identically zero on the chosen interval. Finding a family of orthogonal functions is important in order to identify a basis for a function space. Once a basis is found, all functions in that particular function space can be expanded with respect to the orthogonal functions. The choice of trigonometric functions sine and cosine lead to Fourier analysis which is a central tool for analyzing periodic signals. Other families of orthogonal functions, such as orthogonal polynomials, find application in numerical techniques such as least-squares approximations, Gauss and related quadrature, iterative methods in linear algebra, the detection of singularities, integral equations, and wavelets in medical diagnostics, but also in optimal control, dynamical systems, gas dynamics, integrable systems, and random matrices. Different examples of orthogonal functions are provided with two choices of weight functions on two different intervals. The functions and their weighted product are displayed together with the signed area. The inner product with the chosen weight is computed to test for orthogonality.