Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

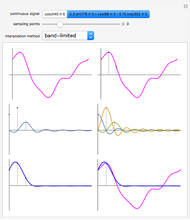
Approximating Continuous Functions with Haar Approximations

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

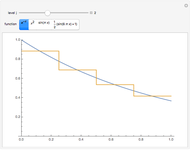
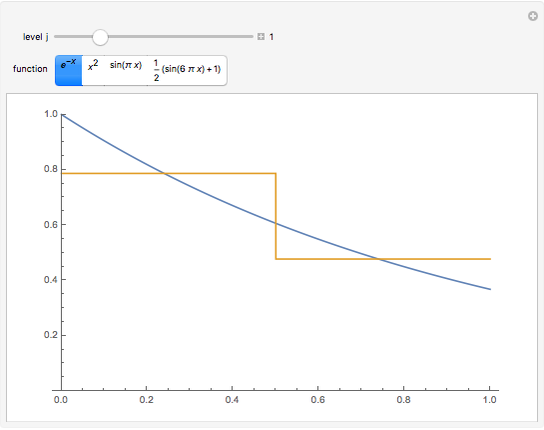
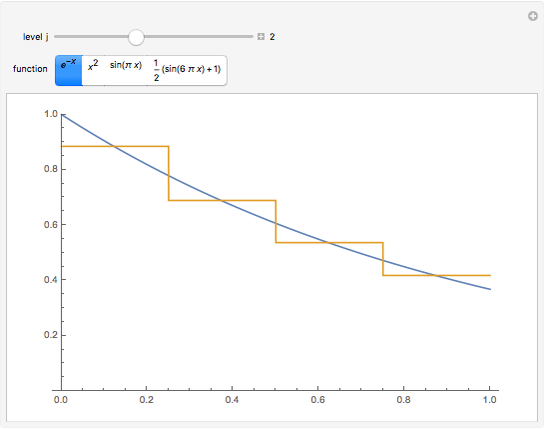
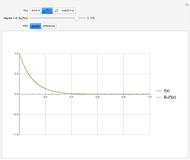
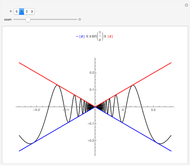
The Haar scaling function is defined by

[more]

On the Haar space is spanned by , where is a non-negative integer. A continuous function can be approximated by a piecewise constant function by projection into Haar space.

[less]

Contributed by: Sijia Liang and Bruce Atwood  (July 2011)
(Beloit College)
After work by: Helmut Knaust
Open content licensed under CC BY-NC-SA

Snapshots

Details

Since the basis functions form an orthonormal set, the approximation of in is , where is determined by the inner product . Students should ask themselves, "What is the interpretation of the projection of into ?" For more information, see Hemut Knaust, "Multi-Resolution Analysis for the Haar Wavelet."

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send