Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

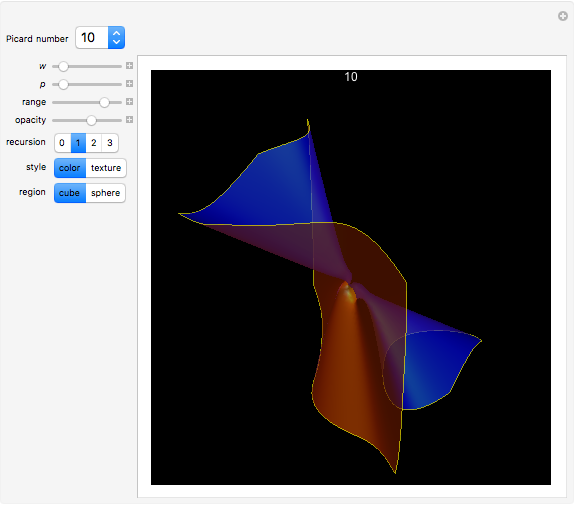
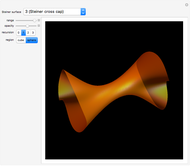
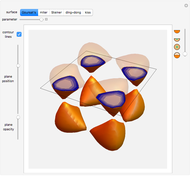
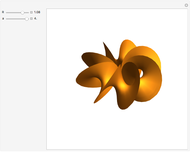
Picard Numbers of Quintic Surfaces

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

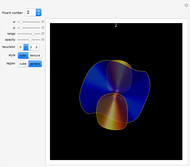
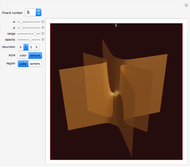
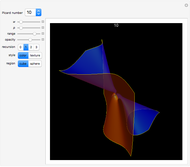
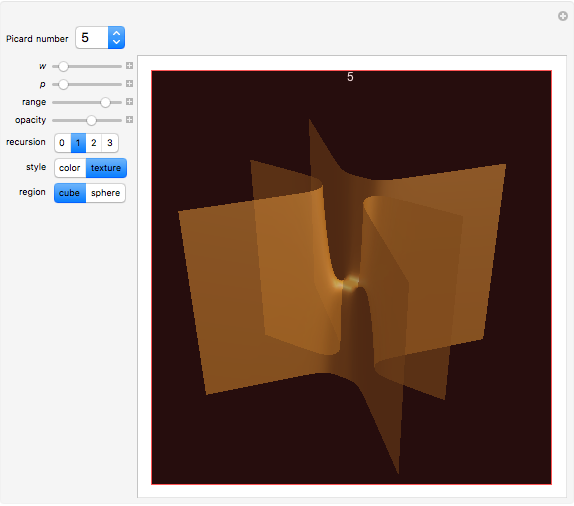
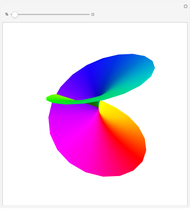
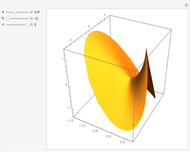
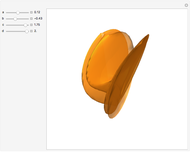
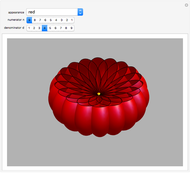
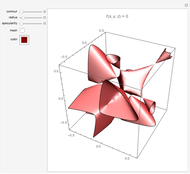
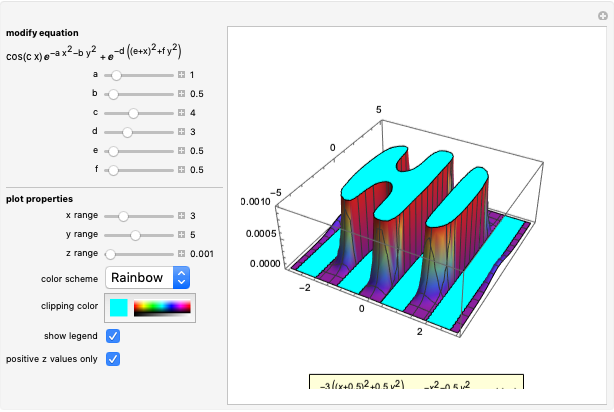
An algebraic surface is defined as the set of points that satisfy a polynomial equation . The Picard number for an algebraic surface is a measure of the complexity of the curves on the surface. Algebraic surfaces with Picard numbers 1 to 45 are presented according to [1] and [2] containing parameters and .

Contributed by: Enrique Zeleny (September 2013)
Open content licensed under CC BY-NC-SA

Snapshots

Details

More formally, the Picard number is the finite rank of the nonsingular complete variety of a sheaf cohomology group [3].

References

[1] M. Schuett, "Quintic Surfaces with Maximum and Other Picard Numbers." arxiv.org/abs/0812.3519.

[2] M. Schuett, "Picard Numbers of Quintic Surfaces." arxiv.org/abs/1308.2525.

[3] Wikipedia. "Picard Group." (May 6, 2013) en.wikipedia.org/wiki/Picard_group.

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send