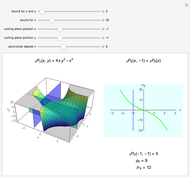
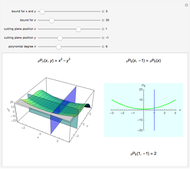
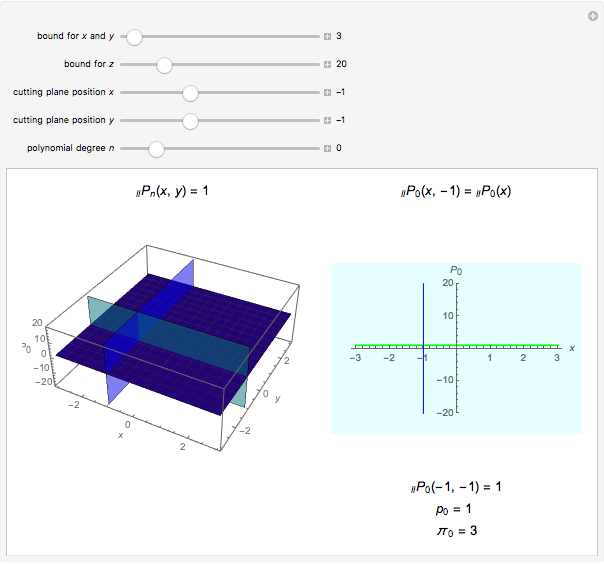
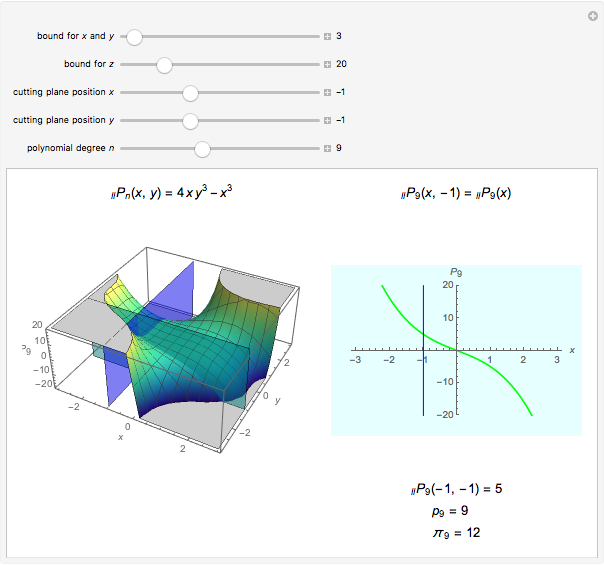
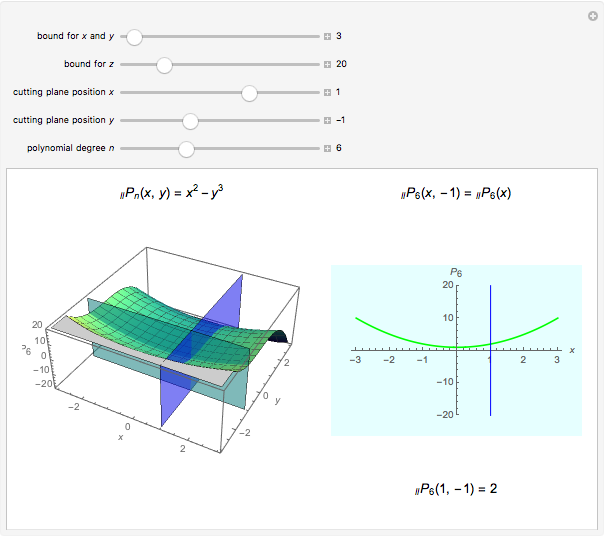
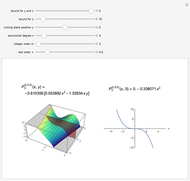
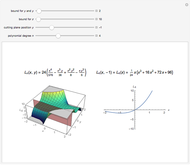
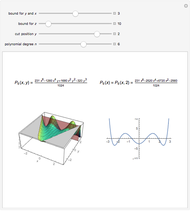
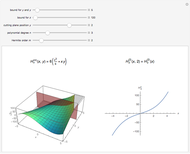
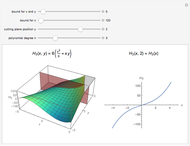
On the left of each graphic is a three-dimensional plot of a lacunary Legendre polynomial in two variables 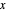and 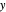. On the right is a two-dimensional plot of the surface cut by a plane perpendicular to the axis. Also shown is the trace of a plane perpendicular to the 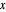axis. These lacunary Legendre polynomials are defined in the Details.