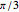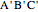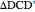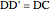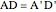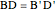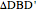Wolfram Demonstrations Project

12,000+ Open Interactive Demonstrations
Powered by Notebook Technology »

Pompeïu's Theorem

Initializing live version
Download to Desktop

Requires a Wolfram Notebook System

Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.

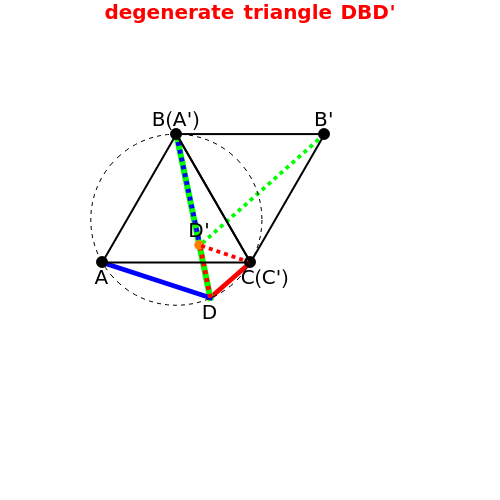
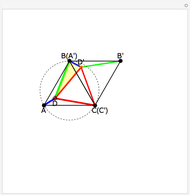
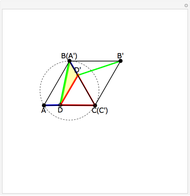
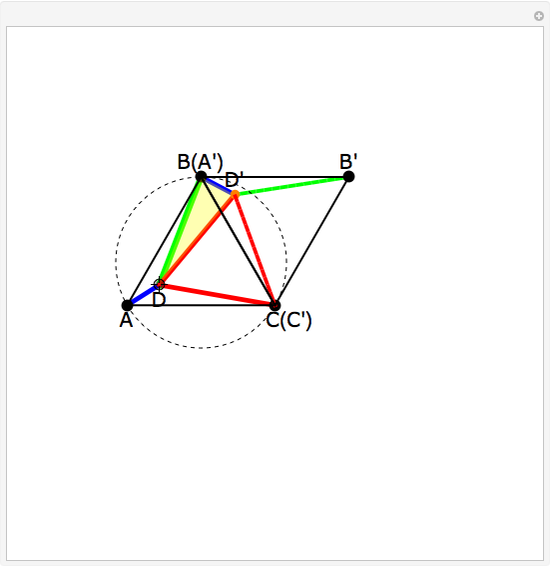
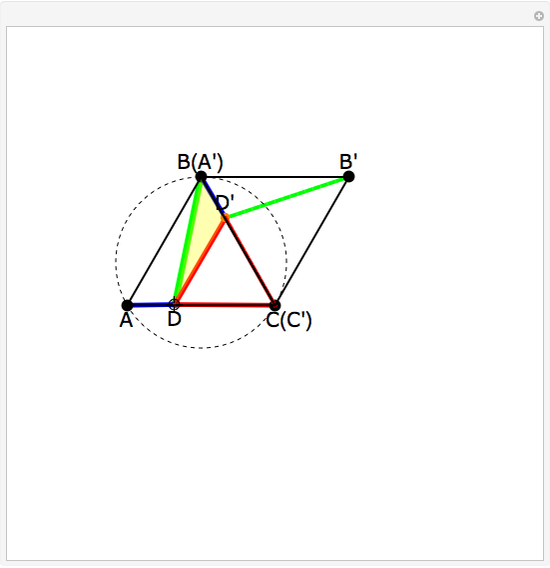
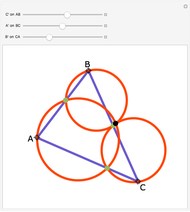
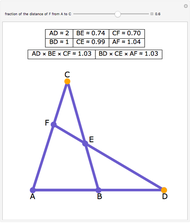
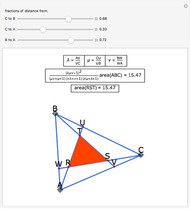
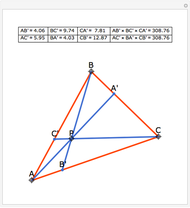
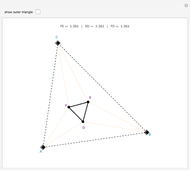
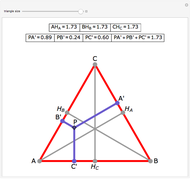
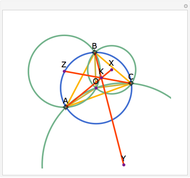
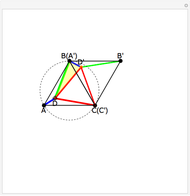
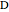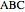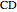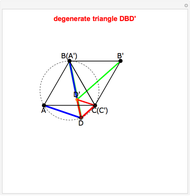
This Demonstration gives a proof of Pompeïu's theorem: If is a point in the plane of the equilateral triangle , then there exists a triangle with side lengths , , and unless 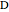lies on the circumcircle of the triangle 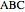, when the triangle is degenerate.

[more]

We rotate the equilateral triangle around the point by an angle of . This gives the triangle . As and , is equilateral, so . Also, and , so we have constructed whose sides have the same lengths as , , and .

[less]

Contributed by: Igor Mandric and Ecaterina Bunduchi (March 2011)
(Moldova State University)
Open content licensed under CC BY-NC-SA

Snapshots

Details

Embed Code

Take advantage of the Wolfram Notebook Emebedder for the recommended user experience.

Related Demonstrations More by Author
Browse all topics
Feedback (field required)
Email (field required) Name
Occupation Organization
Note: Your message & contact information may be shared with the author of any specific Demonstration for which you give feedback.
Send