QR Decomposition

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
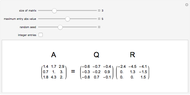
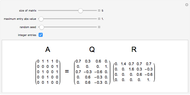
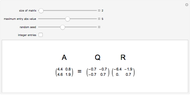
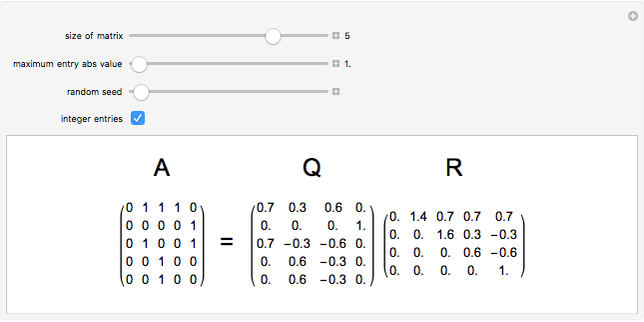
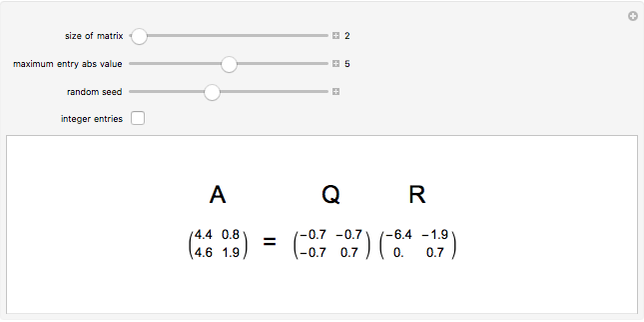
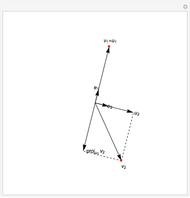
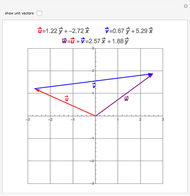
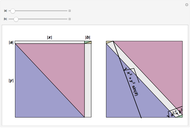
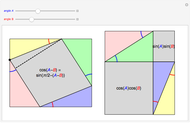
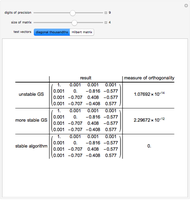
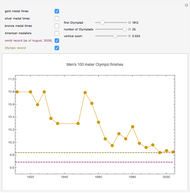
The QR decomposition of a square matrix A factors A as the product of an orthogonal matrix Q and an upper triangular matrix R. An orthogonal matrix is a matrix whose columns are mutually orthogonal unit vectors and so satisfies 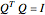 , where
, where 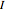 is an identity matrix, and an upper triangular matrix is a matrix whose entries below the main diagonal are all zero. The matrix Q is the result of performing the Gram-Schmidt process on the columns of A. The Mathematica function QRDecomposition[a] accomplishes this factorization, producing the list
is an identity matrix, and an upper triangular matrix is a matrix whose entries below the main diagonal are all zero. The matrix Q is the result of performing the Gram-Schmidt process on the columns of A. The Mathematica function QRDecomposition[a] accomplishes this factorization, producing the list 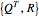 .
.
Contributed by: Chris Boucher (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
detailSectionParagraphPermanent Citation
"QR Decomposition"
http://demonstrations.wolfram.com/QRDecomposition/
Wolfram Demonstrations Project
Published: March 7 2011