Quantum Computer Search Algorithms

Requires a Wolfram Notebook System
Interact on desktop, mobile and cloud with the free Wolfram Player or other Wolfram Language products.
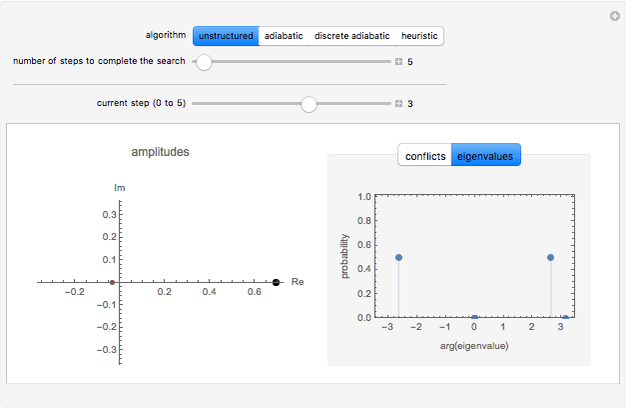
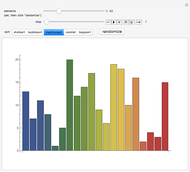
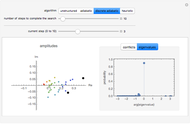
Quantum computers use subtle physical behaviors of quantum mechanical systems for computing. Such computers may solve some problems, such as integer factoring, dramatically faster than conventional machines. Two major challenges for quantum computing are building the machines and developing algorithms exploiting their unique capabilities. Only a few quantum computer algorithms have been invented so far, and they can have counterintuitive behaviors. This Demonstration visually compares four quantum computer search algorithms. The left plot shows the amplitudes of the quantum state during the search, with the large black points corresponding to the two solutions of the problem. The right plot shows the probability distribution among either the number of conflicts in the possible results or the eigenvalues of the quantum search operator. Results with zero conflicts are the solutions.
Contributed by: Tad Hogg (March 2011)
Open content licensed under CC BY-NC-SA
Snapshots
Details
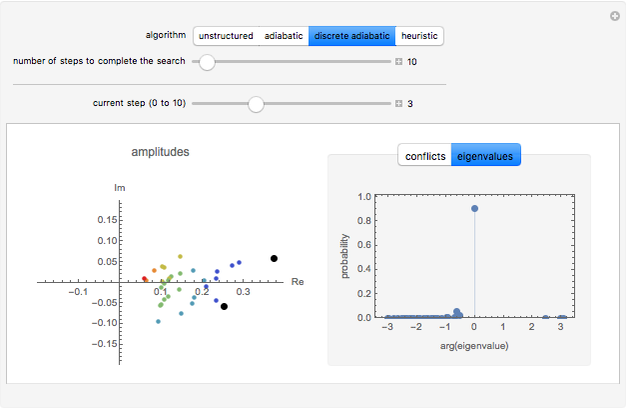
Snapshot 1: discrete adiabatic algorithm reducing amplitudes in high-conflict results
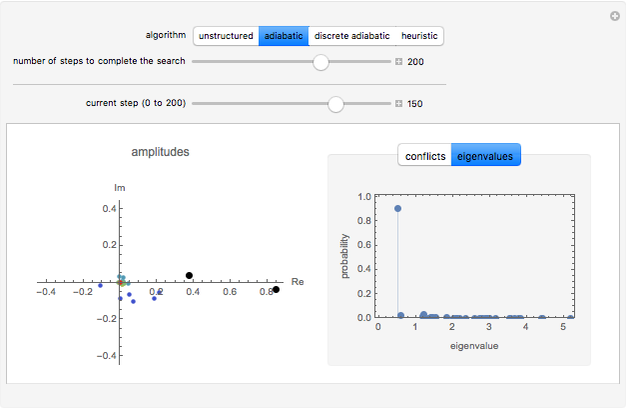
Snapshot 2: adiabatic algorithm near end of search
Snapshot 3: unstructured algorithm with high probability for finding a solution
This Demonstration shows how different quantum algorithms solve a small satisfiability problem with two solutions. The plots provide several views on how the computation changes at each step of the algorithms.
Quantum computer algorithms for combinatorial search problems operate on a vector of complex numbers (called amplitudes), with one number for each possible search result. Each algorithm in this Demonstration starts with equal amplitudes in this vector. The algorithms run for a prespecified number of steps, each multiplying the vector by a unitary matrix, which may be different for each step.
After completing all the steps, observing the quantum state produces a definite result, which may or may not be a solution and may be different if the algorithm is run again. The probability of observing each result is equal to the squared magnitude of its corresponding amplitude. Thus, the algorithms are probabilistic and require a final check of whether the observed result is in fact a solution; if not, the algorithm must be repeated.
Ideally, an algorithm gives a high probability to obtain a solution with only a few steps. The high probability means repetitions are unlikely, and using a few steps means each run of the algorithm completes rapidly.
These probabilistic algorithms are best suited to search problems where finding a solution is difficult but testing the validity of a proposed solution is easy with conventional computers. Satisfiability is one such problem, and is among the well-studied class of NP-complete combinatorial search problems. A satisfiability problem consists of finding assignments to Boolean variables that satisfy a logical formula. A problem with  variables has
variables has 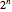 assignments, so a quantum algorithm for an
assignments, so a quantum algorithm for an  -variable satisfiability problem involves vectors and matrices of size
-variable satisfiability problem involves vectors and matrices of size 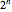 . In this Demonstration, the logical formula involves 5 variables and is a conjunction of 21 clauses, each of which involves 3 of those variables. A solution must satisfy all the clauses. The algorithms use the number of unsatisfied clauses, or conflicts, to define their unitary matrices.
. In this Demonstration, the logical formula involves 5 variables and is a conjunction of 21 clauses, each of which involves 3 of those variables. A solution must satisfy all the clauses. The algorithms use the number of unsatisfied clauses, or conflicts, to define their unitary matrices.
Simulating quantum algorithms, as done in this Demonstration, involves an exponential slowdown in processing speed and an exponential increase in memory compared to running the algorithm on a quantum computer. Thus, simulations are limited to small problems, up to about 30 variables with current computers. By contrast, conventional heuristics for the satisfiability problem often can find solutions for problems with thousands of variables. Thus, even if quantum search algorithms have a theoretical advantage for some large problems, which is an open question, the advantage will only become practically relevant if quantum computing technology allows manipulating at least thousands of bits. Such technology is well beyond currently demonstrated capabilities for quantum computers. Simulations have one major advantage: allowing visualization of the state of the quantum computer during its operation. In an algorithm running on an actual quantum computer, neither the amplitudes nor the solution probabilities would be observable.
The top two controls of this Demonstration allow you to select among four quantum algorithms and to specify the total number of steps the algorithm will use. The bottom control varies the operation step of the selected algorithm, starting from the uniform initial amplitudes (step 0) and ending with the total number of steps specified with the second control.
The left plot shows the amplitudes in the complex plane, colored according to the number of conflicts of the associated assignment. The large black points have no conflicts (i.e., are solutions). Colors from blue to red indicate assignments with an increasing number of conflicts.
The tabs on the right allow you to select one of two plots of probability distributions. The first tab shows the probability in assignments with each number of conflicts in the problem. In most cases, the algorithms increase the probability in assignments with few conflicts. Thus, even if a solution is not found, the algorithm will likely produce an assignment with only a few conflicts. The second tab shows the probability in each eigenvalue of the algorithm's matrix for the corresponding step. This plot is most relevant for the two adiabatic methods, which rely on keeping most of the probability in a single eigenstate by only changing the matrix slightly from one step to the next. The algorithms use unitary matrices, whose eigenvalues are complex numbers with unit magnitude. The plot shows the argument of these eigenvalues, except for the adiabatic algorithm where the plot uses eigenvalues of the corresponding Hamiltonian instead.
The four algorithms and links to further information are:
1) unstructured: uses the same operator for every step and has the solution probability changing sinusoidally with the number of steps; so using more steps can give worse performance. For small problems, such as the one used in this Demonstration, this algorithm has the best performance. See L. Grover, "Quantum Mechanics Helps in Searching for a Needle in a Haystack," Physical Review Letters, 79(2), 1997 pp. 325–328.
2) adiabatic: a discrete-step approximation to the continuous evolution of a slowly changing Hamiltonian; with probability for a solution guaranteed to approach one as the algorithm running time (and hence number of steps) increases. See E. Farhi, J. Goldstone, S. Gutmann, J. Lapan, A. Lundgren, and D. Preda, "A Quantum Adiabatic Evolution Algorithm Applied to Random Instances of an NP-Complete Problem," Science, 292(5516), 2001 pp. 472–475.
3) discrete adiabatic: uses slowly changing unitary matrices without attempting to approximate continuous evolution; with probability for a solution often approaching one as the number of steps increases. The method often gives high solution probability with relatively few steps, but lacks the theoretical guarantee of the continuous evolution. See T. Hogg, "Adiabatic Quantum Computing for Random Satisfiability Problems," Physical Review A, 67(2), 2003.
4) heuristic: uses operators theoretically predicted to have good performance, on average, for satisfiability problems whose clause to variable ratio is near 4.25, as is the case for the problem used in this Demonstration. Unlike the other algorithms, the solution probability is not close to one, but can be fairly large in just a few steps, giving good performance even accounting for a few repetitions. See T. Hogg, "Quantum Search Heuristics," Physical Review A, 61(5), 2000.
A Java demo shows these algorithms with larger problems.
Permanent Citation
"Quantum Computer Search Algorithms"
http://demonstrations.wolfram.com/QuantumComputerSearchAlgorithms/
Wolfram Demonstrations Project
Published: March 7 2011